黒木玄 Gen Kuroki
- いいね数 389,756/311,170
- フォロー 995 フォロワー 14,556 ツイート 293,980
- 現在地 (^-^)/
- Web https://genkuroki.github.io/documents/
- 自己紹介 私については https://twilog.org/genkuroki と https://genkuroki.github.io と https://github.com/genkuroki と https://github.com/genkuroki/public を見て下さい。
2022年01月27日(木)

井上智洋さんの記録
教科書(例【マンキューのマクロ】)には「又貸し説」とやら(定義が不明)が書いてあり、【又貸ししか頭にない人は信用創造の部分をしばしば忘れる】ということになっているらしい。
この独特の「又貸し説」という言い方がローカルな共通了解になっているサークルがあるっぽい。 twitter.com/genkuroki/stat... pic.twitter.com/WptPdyUz1Q
タグ:
posted at 23:53:18


@tomo_monga @kikumaco ええと、井上智洋さんは特殊な自説の証拠を自分で出すことができないということでしょうか?
井上さんが自力で出せないのであれば仕方がないことです。
もしもそうならば、井上さんは特殊な自説の証拠を自分で出すことができなかったという確定情報を私が拡散してこの会話は終了となります。
タグ:
posted at 23:42:14

@ono_k @genkuroki 自分は、左手の拳骨の、人差し指の第1関節から小指に向かって数え、でっぱりが31日だよと、先輩から教わりました。
人差し指が1で小指まで行ったら7、折り返して小指を8と数えて戻り、中指で12となる、そんな方法です。
タグ:
posted at 21:39:24

最初は奇数が大の月、偶数が小の月、
夏休み、宿題やっていなくて泣くのが8月31日だから、それ以後は偶奇が逆転する
で覚えてしまった。 twitter.com/genkuroki/stat...
タグ:
posted at 21:28:05


既に何人から突っ込まれているけど、それ、カタストロフィーじゃないんじゃ…。「カタストロフィー」に<浄化>って振っているから「カタルシス」なわけですが…。幻冬舎、誰も見ていないのかしら…。『40代になると「カタストロフィー」が得られるようになる理由』 gentosha-go.com/articles/-/40413
タグ:
posted at 18:59:15

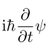
uchitode2014@量子力学同好会 @ruchitode44
にしむくさむらい、簿記の教科書で見ました(覚えた twitter.com/genkuroki/stat...
タグ:
posted at 18:42:36

 非公開
非公開
タグ:
posted at xx:xx:xx




『望月さんの紹介でお会いしたのだから、すべてのきっかけは彼女』
『なぜ彼女はこの場に来ないのですか』
『会社の上層部に、もう一切かかわるなと止められている』
『望月記者にも話を聞こうと自宅』
『「週刊文春」と名乗ったとたんに切られ、あとは一切応答なし』
ミステリと言う勿れ
タグ:
posted at 14:07:23


『昨年12月』
『河村氏は謝罪』
『赤木さんは不信感を強め』
『夫と私は大きな組織に人生を滅茶苦茶にされたけれど、今、あの時と同じ気持ち』
『ドラマ版のあらすじを見たら私たちの現実そのまま』
文春記者映画化されたら、アカデミー賞総なめじゃないの?
え?エントリーされない??何で???
タグ:
posted at 14:05:20


『赤木雅子さんが夫の遺書を公表』
『望月記者が手紙』
『ドラマ版「新聞記者」制作へ』
『赤木俊夫さんの精神科医に河村氏が物言い』
『不信感を抱いた赤木さん“また真実を歪められかねない”と協力拒否』
『要望をほぼ受け入れず制作進めるとメール』
文春記者、映画化はよ
bunshun.jp/articles/-/51663
タグ:
posted at 14:00:46


#統計 極端な意見のどちらかの選択を迫るのではなく、双方の良い点を相互補完的に使えば良いとするLehman (1993)の考え方の方を広めた方が我々の将来のためには良いと思いました。
この点についてまずそうな記述のある入門的教科書は結構あるのではないか?
errorstatistics.files.wordpress.com/2013/11/lehman... pic.twitter.com/XnZW7oNznO
タグ: 統計
posted at 13:44:39

検定の理論についての偉い人が検定に関する「Fisher流 vs. Neyman-Pearson流」問題について何を述べているかを検索すると、仮設検定に関する有名な教科書の著者でもあるLehmanさんによる穏健で建設的な意見を読むことができます。
↓ twitter.com/genkuroki/stat... pic.twitter.com/CZ4OWZ9FnT
タグ:
posted at 13:40:50

昔ながらの検定や信頼区間に関する解説がミスリーディングになり易い理由として、主義に基く極端な考え方の選択を迫る悪しき慣習があるように思えます。
例えば、検定について「Fisher流」と「Neyman-Pearson流」のどちらの主義に従うのか、を強く問題にすることはある種の伝統芸能になっている。続く
タグ:
posted at 13:36:56

テンプレ:以前~という考え方を~で解説したが、{誤解を招く説明になっていた, ひどく雑すぎた, 間違っていた, 頭が狂っていた, …}。新たに勉強し直したことを以下で説明する。~
「このテンプレをずうずうしく繰り返せば良いだけ」と踏ん切りがつけば色々楽になる。
タグ:
posted at 13:32:19


#統計 検定と信頼区間の関係は「数理統計学」の教科書ではしっかり解説されているし、ASA声明のP値の説明でのキーワードは「統計モデル」だし、Rothmanさん達の疫学の有名教科書や以下のリンク先で紹介した論文にも信頼区間の有効な使い方が書いてある。
諸々の有益な情報をどう拡散するかが問題。 twitter.com/genkuroki/stat...
タグ: 統計
posted at 13:19:29


#統計 以下のリンク先スレッドに「数理統計学」と題された有名な教科書達に検定と信頼区間が表裏一体であることの説明があることの証拠がある。
竹内啓『数理統計学』
竹村彰通『現代数理統計学』
久保川達也『現代数理統計学の基礎』
には載っている。これらは超有名な教科書! twitter.com/genkuroki/stat...
タグ: 統計
posted at 13:08:21


#統計
❌95%信頼区間の95%は確率ではなく割合だ
という誤解を広めている人(達)は、現実に得たデータの数値は確定しているという理由で
❌データの確率的揺らぎ由来の確率を考えるのはおかしい
とする誤りを犯しているのだと思います。
「統計モデル内部での確率」という考え方が足りない。 pic.twitter.com/LcTSDGfUQa
タグ: 統計
posted at 12:42:58

#統計 「統計モデル」(例えば正規分布モデルは典型的)の存在を心の中から消してしまっているせいで、現実に得たデータの数値は確定しているという理由で
❌データの確率的揺らぎ由来の確率を考えるのはおかしい
のように間違った方向に進んでしまうのです。
ASA声明でのP値の解説を理解していない! pic.twitter.com/K0BSFYe8XA
タグ: 統計
posted at 12:39:24

#統計 95%信頼区間の95%は「P値が5%以上になる確率」なのですが、その確率は統計モデル内部での確率になります。
この点がASA声明 www.biometrics.gr.jp/news/all/ASA.pdf でのP値の解説(添付画像)にもろに繋がります。
ASA声明ではP値の説明で「統計モデル」が重要キーワードになっています。この点が非常に重要! pic.twitter.com/xEwRPolh3G
タグ: 統計
posted at 12:35:24




#統計 添付画像はRothman-Greenland-Lash Modern Epideomology 3rd edition 2008 より。
Fisher検定型のP値函数のグラフは添付画像のようなグラフにはなりません。
分割表の独立性(オッズ比=1)のχ²検定を1以外の場合に拡張して作ったP値函数のグラフは添付画像のような形になります。 pic.twitter.com/THa5taYjzp
タグ: 統計
posted at 12:14:58

#統計 添付画像はRothman-Greenland-Lash Modern Epideomology 3rd edition 2008 より。
で、2×2の分割表について「オッズ比は○○である」という仮説達のP値のFisher検定版の計算にはFisherの非心超幾何分布が必要になるので入門的教科書にも解説がないとまずいと昨晩考え始めてしまったわけ。 twitter.com/genkuroki/stat... pic.twitter.com/74b19sjOsq
タグ: 統計
posted at 12:10:48


算数・数学を理解している大人ですら理解できないものを小学生に理解させるなんて無理だよね。
こんなくだらないこと理解できなくても問題ないってわかっている小学生ならいいけど、そうじゃない子が「理解」させられるのは可哀そう。 twitter.com/edgeofstreet91...
タグ:
posted at 12:02:14



#統計 「差がない」という仮説のP値だけではなく、「差が○○である」という仮説のP値を○○に対応させるP値函数(信頼区間函数)を使って図を描いて説明すると分かり易くなります。添付画像は
Rothman-Greenland-Lash Modern Epideomology 3rd edition 2008
にある説明です。分かり易いです。 twitter.com/genkuroki/stat... pic.twitter.com/r5cOQI3j2A
タグ: 統計
posted at 11:48:46


#統計 「95%信頼区間と臨床的に意味のある差」の関係を理解するためには、
ASA声明で解説されているP値に関する考え方
と
信頼区間=P値がα以上になるパラメータの範囲
という信頼区間の定義を組み合わせる必要があるのに、信頼区間を「P値以外のアプローチ」だとみなす人達がそれを妨げている。 twitter.com/cochranejapan/...
タグ: 統計
posted at 11:37:32

#統計 P値については、有名で教育的なASA声明
www.biometrics.gr.jp/news/all/ASA.pdf
があるのですが、信頼区間を「P値以外のアプローチ」に分類してしまっている点は良くないと思いました。
信頼区間はP値がα以上になるパラメータの範囲なので、どう考えても「P値を使うアプローチ」の一種です。 pic.twitter.com/Dxw1iTCiiY
タグ: 統計
posted at 11:32:50






#統計 手もとにある入門的教科書で、信頼区間が「データによって棄却されないモデルのパラメータの範囲」であることを解説しているものは皆無。
数理統計の教科書には載っていますが、その知識を最も必要としている人達に情報が届いていない感じ。 twitter.com/cochranejapan/...
タグ: 統計
posted at 03:58:58



#統計 以上のようなことを深夜に考えていて
それじゃあその方針で、例えば
「比率の違いの検定と信頼区間」
についてどー解説するのか?
と思い、比率の違いをオッズ比で表し、信頼区間を「検定経由」で計算するためには、Fisherの非心超幾何分布が必要なことに気付いて以下のリンク先の発言に至る。 twitter.com/genkuroki/stat...
タグ: 統計
posted at 03:33:58






#統計 #Julia言語 のDistributions.jlでのFisherの非心超幾何分布の実装
↓
github.com/JuliaStats/Dis...
超幾何分布のシンプルさと比較すると、Fisherの非心超幾何分布は全然別の世界に見える。
posted at 02:34:04

#統計 超幾何分布の解説は載せるが、Fisherの非心超幾何分布の解説を載せないということは、表と裏が同じ確率で出るコイントスの分布の解説は載せるが、一般のベルヌーイ分布の解説は載せないということに対応している。
Fisherの非心超幾何分布のウィキペディア
↓
en.wikipedia.org/wiki/Fisher%27...
タグ: 統計
posted at 02:29:14


 非公開
非公開
タグ:
posted at xx:xx:xx






