黒木玄 Gen Kuroki
- いいね数 389,756/311,170
- フォロー 995 フォロワー 14,556 ツイート 293,980
- 現在地 (^-^)/
- Web https://genkuroki.github.io/documents/
- 自己紹介 私については https://twilog.org/genkuroki と https://genkuroki.github.io と https://github.com/genkuroki と https://github.com/genkuroki/public を見て下さい。
2023年01月08日(日)

【水星の魔女】
season1最終回を記念してYOASOBI/祝福をサックスとピアノにアレンジして実演しました。
ピアノは川合愛美さん@k_manami_piano
今回はYouTubeにfullをあげます。またツリーにぶら下げておきます!
(ここまで下書き 以下視聴後)
そういえばガンダムだった
#水星の魔女 #G_Witch pic.twitter.com/sMUWAaFliq
posted at 23:12:30

@panlepan @Cshearer41 The elegant solution of my wife: pic.twitter.com/cBqN07XNix
タグ:
posted at 23:06:25


すごい!!
ピアノ職人さんに感謝!ってなった!
【一気見】ヤマハのグランドピアノを徹底オーバーホール!作業完全密着しました! youtu.be/S_hUPeNbECY @YouTubeより
タグ:
posted at 20:38:13

 非公開
非公開
タグ:
posted at xx:xx:xx

Julia Lang v1.8.5 Release!!!
🟣🟢🔴
#JuliaLang
github.com/JuliaLang/julia
タグ: JuliaLang
posted at 20:24:51

#Puzzle animated. What's the angle ?
#GeometrySnacks #MathGIF twitter.com/panlepan/statu... pic.twitter.com/Bf8whRBF2h
タグ: GeometrySnacks MathGIF Puzzle
posted at 20:18:47

川合愛美 manami kawai @k_manami_piano
ついに4000人いきました!ありがとうございます🙏🥹
今回は野口さんが出演😊
【ピアノ初心者向け】アップライトピアノの基礎知識、調律師が教えます。 youtu.be/haiVeXDhlE4 @YouTubeより
#サンピアン #ピアノ #調律 pic.twitter.com/E0YN2jhepo
posted at 18:56:52
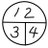
@twinklepoker 右下の下から2行目のxの左に見えているイコールみたいなのは下の分数を約分した2だなあ、と思いながらよ〜く見たら真ん中の青字の「5×5×π=25π×2」ってヤツでした。
まさかこれもウッカリミスとして擁護する人が湧いて出るのかな。
「×2」と書きたくなった瞬間に左にも書き足そうとするのがマトモ。
タグ:
posted at 18:00:55

@genkuroki 遠慮なく面子を潰しに行くのですが、
大体の人が頭がカチコチか、もはや論理的に考えられないので、否定されるんですよねー。
Rとかで簡単に統計解析できるのは良いことですが、理解できてないし、「有意差の有無」だけで議論するのはやめてほしい。
しかも、有意差の有無の解釈も間違ってる始末。
タグ:
posted at 15:17:36

続き。そういう例はt分布とそれに等しい正規分布の組み合わせで作れます。
等分散でもWilcoxon-Mann-Whitney検定の適用が不適切になる場合
↓ twitter.com/genkuroki/stat...
タグ:
posted at 15:16:03

zenn.dev/tmizuho/articl...
【ウィルコクソンの順位和検定 (Wilcoxon rank sum test) は~データに等分散性が仮定できる場合に使用できます。】
これも誤りです。
対称で平均値と分散が一致する2つに確率分布で、Wilcoxonの順位和検定で有意差の出る確率が非常に高くなるものを作れます。続く
タグ:
posted at 15:16:02


例えば、粗雑な統計学的素養しか持っていない査読者によってアクセプトが決定された査読論文の科学的信頼性は低いと社会的に評価されるべきです。教科書についても同様。
タグ:
posted at 15:00:18

標準的な教科書に書いてあるとか、査読論文として発表されているということ自体ではなく、「十分批判的に検討されているか」を強調するのであればまとも。
標準的な教科書に書いてあるとか、査読論文として発表されているということ自体を強調する行為は非科学的な権威主義であり、徹底的に潰すべき。
タグ:
posted at 14:58:08

特に昔からある権威ある著者による影響力が大きそうな教科書ほど、きちんと誤りを指摘して行く必要があると思います。
科学の世界では、標準的な教科書に書いてあるとか、査読論文として発表されているということ自体は正しいことの証拠にならないという当たり前のことを明瞭に認めることが大事。
タグ:
posted at 14:58:07

正規性検定→F検定→t検定としてよいかのように(もしくはそうするべきであるかのように)書いてある教科書や解説については、誰かがリストを作って「誤りが書いてある教科書と解説のリスト」として誰か発表するべきだと思います。
多重検定の問題への対処の仕方が書いてあれば情状酌量の余地有り。
タグ:
posted at 14:53:10

zenn.dev/tmizuho/articl...
【「~等分散性の検定はせずに、いきなりウェルチの t 検定を実施する方がよい」という議論があるようです。一方で、教科書などでは「問題ない」という見方が多いように感じますし、まだ答えが出ているわけではない】
「問題ない」としている教科書の側が間違っています。
タグ:
posted at 14:49:26

#統計
zenn.dev/tmizuho/articl...
【ウェルチの t 検定 (Welch t-test) は~データに正規性が仮定できる場合に使用できます。】
これも既出の誤り。母集団分布の正規性は必須ではない。
(データの正規性の話にしている点もおかしい。)
タグ: 統計
posted at 14:47:19


zenn.dev/tmizuho/articl...
【スチューデントの t 検定 (Student t-test) は~データに正規性および等分散性が仮定できる場合に使用できます。】
これも誤り。
* 正規性は必須ではない。
* 母集団分布に等分散でなくても、等サンプルサイズなら使える。
タグ:
posted at 14:44:26

対応がある場合のt検定は
x₁ - y₁, x₂ - y₂, ..., xₙ - yₙ
型の1つの標本に関するt検定になるので、2群の分散の違いは問題になりません。
x₁ - y₁, x₂ - y₂, ..., xₙ - yₙ の標本平均の分布が正規分布で十分近似されていればt検定を使える。(正規母集団である必要はない)
タグ:
posted at 14:38:23

zenn.dev/tmizuho/articl...
【類似の手法にスチューデントの t 検定がありますが、スチューデントの t 検定とは違って 等分散性の検定は必要ありません。これは、対応のあるデータでは等分散性が仮定できるから、だと理解しています。】
理由の理解が間違っています。
タグ:
posted at 14:34:02


最近書かれた
zenn.dev/tmizuho/articl...
【正規性の仮定に不安があれば、ウィルコクソンの符号順位検定を使っておくと無難といった考え方もあるようです】
もまずいです。Wilcoxonの符号順位和検定も無条件で使える検定法ではありません。
有意差を出すための検定達というまとめ方自体が根本問題。
タグ:
posted at 14:28:52



#統計 伝統に従うと、対応がない2群のt検定については
正規性検定
↓
F検定
↓
t検定
の手順になったりするのですが、
* 多重検定の問題
だけではなく、
* そもそも正規性は必須でない
* 等分散であるか否かと無関係にWelchのt検定は使える
のような事実を無視している点が非常にまずい。続く twitter.com/industrial_ds/...
タグ: 統計
posted at 13:22:19

いいですよねこういうの。
間近でピアノの中身を拝めたり調律体験が出来るイベントとかがあったら仕事ぶん投げて参加しちゃうだろうなあ。長野までひとっ飛び。
GT、本日は休日出勤です。
お疲れ様です。 twitter.com/sunpian_nagano...
タグ:
posted at 12:46:37

#Julua言語
ソースコードと実行結果
nbviewer.org/github/genkuro...
v1.8.4
nbviewer.org/github/genkuro...
v1.9.0-beta2
タグ: Julua言語
posted at 12:34:51

#超算数
mobile.twitter.com/sekibunnteisuu...
これ見る限り、順序指導しても、「○算の授業だから○算」は減っていないようだ。
かけ算順序指導、効果ないんじゃないの?(前々からわかっていたけど)
タグ: 超算数
posted at 12:02:02


#超算数 【お釣りの計算で引き算しか認めない】のは極端にしても、日本の算数教育界の偉い人が足し算でお釣りを渡す方式を馬鹿にする態度をとっていたことがあります。孫引きですが、塩野直道が『日本の暗算』という本でtwitter.com/temmusu_n/stat...、【こちらでは考えられない不手際と思われる方法】と。 twitter.com/esumii/status/... pic.twitter.com/PKg18d0ex8
タグ: 超算数
posted at 09:57:45

「ぼざろ」の一番の人気曲なんだけど、「何億光年離れたところからあんなに輝く」ということはなくって、肉眼で見れる最も離れた天体で数百万光年なんだよとツッコミを入れたくなったらオヤジ。
#ぼっち・ざ・ろっく
www.youtube.com/watch?v=wSTbdq...
タグ: ぼっち
posted at 09:57:30

100倍速くなったら、100倍時間短縮ができるかというと、100倍重い計算をやりたくなるのが研究者のさが。
結果、実行時間は変わらない。
こっちは地球・月系の三体問題。
#JuliaLang #三体問題 pic.twitter.com/c9WTL4Qid4
posted at 09:51:27

美しき太陽・地球系の三体問題のカオス。
単純に計算速度が約10倍速いだけじゃなくて、並列化も容易だから、100倍くらい速くなっている気がする。
#JuliaLang #三体問題 pic.twitter.com/xxf9rbSZfd
posted at 09:48:10

@cauchy6419 【①90ってどこから出たか】
コーシーさんは問題文を読んでいないのですか?
100円出したらおつりが10円と書いてありますよ?
【②55ってどこから出たか】
35+55=90
と式を書いていますよ?
#超算数
タグ: 超算数
posted at 09:05:11

マルチンゲール@データサイエンス×生産技 @industrial_ds
t検定される方は読むと良いと思います。
F検定からの、t検定でも、多重性の問題が起きます。これは意外と意識されていない気がする。 twitter.com/genkuroki/stat...
タグ:
posted at 08:53:06


@genkuroki ほんとそれです…。
これも可能性に過ぎませんがね…。
世の中に蔓延る、間違った手法でアクセプトされた論文や正しそうに見えるように作られたwebページがある以上、厳し目ですが…。
情報が民主化されたことの弊害…。
タグ:
posted at 05:55:29

@kankichi57301 @nabekichi32 「証明は結論に至る論理の連鎖の記述であり、思考の過程の履歴ではない」と学生には伝えています。大学ですが。
タグ:
posted at 05:01:01


i had to tweak my script to get it correct; otherwise twitter was refusing to upload it. pic.twitter.com/XtwrR8oLoX
タグ:
posted at 02:00:26







#統計 Wilcoxonの順位和検定=Mann-WhitneyのU検定の誤用については20年以上前から話題になっており、例えば、粕谷さんがそのことを指摘する論文を書いています。
kasuya.ecology1.org/stats/utest01....
ただし、これ↑を読んで、等分散ならWMW検定が使用可能だと考えるのは誤りです。等分散でもダメな場合がある。
タグ: 統計
posted at 01:55:11






#統計 Welch及びStudentのt検定も使い分けについては
biolab.sakura.ne.jp/welch-test.html
も参照。等分散であるか否かを気にせずにWelchのt検定を使うことに文句をつけられたら、こもウェブページを反論の根拠に使えば良いと思います。
タグ: 統計
posted at 01:55:06






#統計 【3.等分散(似ている)ならStudent's t検定、不等分散(似ていない)ならWelch t検定】は誤り。
そのように解説している人は統計学の初歩を理解していないので要注意。これ、大問題。
Welchのt検定は等分散と不等分散の区別なく使用可能。正規母集団でなくても多くの場合に使用可能。
続く twitter.com/kokusijukensei...
タグ: 統計
posted at 01:54:54

youtu.be/LliT-96R1mQ
講義動画といえば12月に亡くなったKricheverがICMで語ってた代数幾何と可積分系の問題の話、面白そうだと思う。理論を作り出した張本人なので悪いはずがなさそう
タグ:
posted at 01:47:07



たとえば、笑いたい人には次の動画の07:32以降(そこにリンクをはっておく)を見るとよいかもしれません。
iPadでのある楽譜アプリでページをめくる方法がわかります。
youtu.be/1GF6MPS_Opw&t=...
【RP701】最新電子ピアノと電子楽譜を試したら驚きの連発でした。
07:32
他の動画も楽しいです。
タグ:
posted at 00:32:18

サンピアンさん @sunpian_nagano のYouTubeチャンネルが面白すぎ。最近、ずっと見ている。
www.youtube.com/@sunpian_nagano
【YouTubeチャンネルではピアノに興味を持ってもらうことを目標に動画を配信していきます。】
ピアノの構造についてこんなに楽しく解説してくれている動画群が他にあるだろうか?
タグ:
posted at 00:17:51






