7931
- いいね数 45,477/48,405
- フォロー 253 フォロワー 1,023 ツイート 68,505
- 現在地 チーバくんのみぞおち付近
- Web http://wed7931.hatenablog.com/
- 自己紹介 大学院数学専攻→インフラ系システムエンジニア→ちょっとお休み→新しい職場で心機一転。いろんな #数学 を勉強中。専門はリー群の表現論。妻と息子2人で日ハム応援中 #lovefighters 。 #水曜どうでしょう と #ゴリパラ見聞録 が好き。北海道出身/千葉県在住/松坂世代。
2023年02月05日(日)

どちらかというと、数学を使い慣れている人は、特に数学を使う必要がない(定量化できない/数学を使っても特に論理の補強にならない)ような対象に数学を使って「すごそうに見せる」議論に手厳しいと思う。
twitter.com/mixingale/stat...
タグ:
posted at 22:22:03


先生方が高校時代に学んでいないことを教えるということに抵抗があるように思っています。
解析が専門の私は、確率統計を学び直すことに今となっては学問としても教えることとしても抵抗はない。
この抵抗感のようなものは各先生の数学的なバックグラウンドが大き twitter.com/hirokazuohsawa...
タグ:
posted at 21:58:36




国立天文台野辺山宇宙電波観測所。
微弱な電波を捉える天文観測に影響を与えないように、ご協力いただいています。 twitter.com/sth_west/statu...
タグ:
posted at 21:07:45


 非公開
非公開
タグ:
posted at xx:xx:xx

n次元バイナリーベクトル!
n次元立方体(ハイパーキュープ)の辺の個数を答えさせる問題だ
n次元の立方体は(n≧2)
n-1次元の立方体をコピーして
2つのn-1次元の立方体の対応する点を辺で結んで出来るから
その辺の個数は
2×(n-1次元の立方体の辺の個数)+(n-1次元の立方体の点の個数)
か twitter.com/rest_art321/st...
タグ:
posted at 19:55:08


僕の知り合いの白熊どんが、ちくワンのYouTubeに出ました!
メリケンの言葉をあやつる
テルミーキャットも一緒です🐱
youtu.be/g6AHBMm6zEQ pic.twitter.com/OsYpEXGTIm
タグ:
posted at 18:44:11

第一クール終了🔥💪
#GAORA
#lovefighters
www.instagram.com/p/CoRmUq6vCOJ/...
タグ: GAORA lovefighters
posted at 18:14:59


日奈久ちくワン【熊本ご当地VTuber】 @hinaguchikuwan
新しい動画をアップしたワン!
youtu.be/g6AHBMm6zEQ
(ここをクリックだワン!)
今回はTOEIC満点の
テルミー・キャットの
英会話抜き打ちテスト!
かごしま太郎君のお友達の
白熊どんが挑戦してるだワン!
英会話の勉強にもなるワン!!
#ちくワン pic.twitter.com/wolJWaeeVD
タグ: ちくワン
posted at 17:24:54

ぼくも初めて聞いたときはわからなかったなぁ。行列をどうやって定めているか思い出すことが必要。書き込みので十分にわかってるようにも見えますけど。
部分空間の基底をなすベクトルをTで写すと部分空間の基底ベクトル(最初のr個)だけの線型結合になる。だからr列まではr行より下が0になる。 twitter.com/yama_keisuke28...
タグ:
posted at 17:24:42


「どんなに暗記していても有利にならない入試問題を作り続ける vs どんな問題が出ても有利になる暗記対象を探し続ける」のせめぎ合いは,まあきっと不可避であることがゲーム理論で説明できたりするんでしょうね(たがいに最適戦略をとろうとするの巻?)
タグ:
posted at 17:07:43

放物線を不変にする等積アファイン変換の1パラメータ族を考えると、直線が放物線の準線に平行な場合だけについて計算すればよい、ということですね。
上の等積アファイン変換の合成によって「区間の大きさ」は変わりません。 twitter.com/tsujimotter/st...
タグ:
posted at 15:58:07

3月中旬新刊
MITの名物教授ストラング博士“教科書シリーズ”最新刊。
『世界標準MIT教科書 ストラング:教養の線形代数』
松崎 公紀/平鍋 健児/訳(近代化学社)
従来の書籍とは異なり、ベクトル空間の概念をいち早く学ぶことで線形代数の全体像が見通しやすくなり、飛躍なく諸概念の理解を深めていける
タグ:
posted at 14:55:21



tsujimotter 日曜数学者 @tsujimotter
いわゆる1/6公式って「与えられた二次関数と直線の囲む面積」は、(直線によらずに)囲んだ区間の大きさだけで決まることを主張しているわけなんですが、それって結構非自明で面白いですよね。
(さらにいえば、面積の大きさは囲んだ区間の大きさの3乗に比例するというのも面白い。)
タグ:
posted at 12:27:40
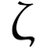
1次独立の定義は言えないけど、ℝ^3の3つのベクトルが1次独立であることを示す問題を出されたら、3つのベクトルを並べた行列の行列式が0でないことを確かめようとする
これ、「きはじ」の大学生版だよな……
タグ:
posted at 11:53:41

行列の積においてAB=1が成り立てばBA=1なことって結構面白いと思うんだけど、線形代数の教科書ってあんまこう言う弱め方の話は強調してない気がする 混乱を招きやすいからかな
タグ:
posted at 11:29:52



おはようございます😊やっぱり無理でした…。「知らないふり」をするために、まだ教科書で定義されていないことは忘れようとするアタマになっています。集合そのものについてのトピックは今の教科書が終わってからかな。不器用なアタマです😓 twitter.com/dtwlbgy33cttgk...
タグ:
posted at 09:35:39







