黒木玄 Gen Kuroki
- いいね数 389,756/311,170
- フォロー 995 フォロワー 14,556 ツイート 293,980
- 現在地 (^-^)/
- Web https://genkuroki.github.io/documents/
- 自己紹介 私については https://twilog.org/genkuroki と https://genkuroki.github.io と https://github.com/genkuroki と https://github.com/genkuroki/public を見て下さい。
2017年11月19日(日)



@Zi_kade @sekibunnteisuu 【1000にmの単位があって、3には単位はないと考えると、掛け算の順番はどちらでも良いように感じるのです】
不可解です。
「1000にmの単位があって、3には単位はない」ならば、2年生用のルールによれば
「1000×3 のみが正解」となる筈ではありませんか?
#掛算
タグ: 掛算
posted at 23:34:09

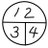
@sekibunnteisuu @genkuroki @tyoukimukou 確か3.05より大きいことの証明だったと思いますから、正8角形で十分示せると思いますよ。ポイントは円周率が円周÷直径であることを忘れずにいることくらい。3.1より大きいことは正12角形で大丈夫だと思います。
タグ:
posted at 22:51:36


#統計 #JuliaLang KL情報量と(WAIC-T_true)/(2n)の揺らぎは大きなサンプルサイズではほぼ逆方向になることを証明できます。
posted at 22:45:48

#統計 #JuliaLang WAICがジャンプする例の3つ目。以上の3つはすべて同じサンプルです。 pic.twitter.com/Kc5xc6uoGN
posted at 22:43:27

@yuukarin39 【かけ算ダメ派の唯一の正論は「ひっくり返したら単位がかわる(3皿×5個だと皿の数が出る)」だと思うので面積図はかけない】
なるほど。
それはそうですね!
ありがとうございます。#掛算
タグ: 掛算
posted at 22:42:40

#統計 #JuliaLang WAICがジャンプする例の2つ目 pic.twitter.com/TQ32JXRz4K
posted at 22:42:03

#統計 #JuliaLang WAICが一斉に上に大きくジャンプする例。右側に「外れ値」っぽい数値がサンプルに追加された瞬間にジャンプしているように見える。こういうことも起こりえるということ。 pic.twitter.com/0DGEa9CBS9
posted at 22:41:04

@yuukarin39 「面積図を描いても、全体量×割合 速さ×時間などの順序を墨守する」という方針でやれば、ボロは出ないのではないでしょうか?
( 縦×横 で書くことに合うように、あらかじめ向きに配慮すれば完璧 )
もしボロが出ている例があれば、是非とも我が資料集に収集したいです。 #掛算
タグ: 掛算
posted at 22:31:01

@sekibunnteisuu @tyoukimukou @Syance_158 π/6 = arctan(1/√3) と arctan(x) のテイラー展開(剰余項付きテイラーの定理)の組み合わせなら、現実的な計算時間で結構な精度が出ます。他にもやり方は無数にあると思います。必要なだけ足して精度を出して、誤差の絶対値を上から評価すれば終わり。本質的に∫_0^x dt/(1+t^2)の近似計算。
タグ:
posted at 22:30:08

@yuukarin39 【大手出版社なら違反しないように気を配っている】
ちなみにリンク先の掲示板に貼った画像の本は、翌年の版では改め(?)られていました。 #掛算
タグ: 掛算
posted at 22:22:52

@yuukarin39 ありがとうございます。
【面積図を使って】とのことですが、大手出版社なら、面積図を描いたときも2年生ルールに違反しないように気を配っているように思います。
論者によっては「面積図を描いたあとは気にしない」という猛者もいますが。
#掛算
8254.teacup.com/kakezannojunjo...
タグ: 掛算
posted at 22:20:17

現在の日銀には片岡剛士さん以外に「ガッツのあるリフレ派」は見当たらない…雨宮?中曽?違う違う。いわたきくお?非ケインズ効果を認めるような発言もしてて「ガッツのあるリフレ派」から「岩田先生も白くなった」と批判されてたから違うかと。構造失業率推計誤りを指摘して現状維持ってドM? twitter.com/shinchanchi/st...
タグ:
posted at 22:10:54

#仮面ライダービルド 今日、蔵本モデルが出たのと時を同じくして、ストロガッツ先生たちの
二ホンアマガエルの同期の論文が。
www.nature.com/articles/s4146... Oscillators that sync and swarm
タグ: 仮面ライダービルド
posted at 22:09:49

@yuukarin39 いきなりで失礼します。
私は #掛算 の順序どうでも良いと思う側です。
【平均や割合の問題を】
その論点、どの様に順序アリ派を追いつめられるのでしょうか?
割合の問題は「 全体量×割合 」で統一されている(彼ら的には)と思うのですが。
タグ: 掛算
posted at 22:03:44

#掛算 #超算数 ↓とあわせて報告されている事例は今のところ2例のみで、極めてレアケースだと思われます。報告事例の数としては、「長方形の面積を横×縦でバツ」の方が多い。
6828.teacup.com/amajima/bbs/229
posted at 22:03:39

#掛算 #超算数 「4人に3個ずつだと何個?」を「4×3の順序でないと駄目。問題文に出てきた順じゃないと駄目」と教えるケースがあるようです。 twitter.com/HighSpeedKou/s...
posted at 22:00:33

片岡剛士さんはYCCを現状維持の言い訳と批判的でコミットメント強化に加え量質金利の強化を主張。上念日銀総裁で30万円配るには日銀法改正伴うため、安倍晋三君に高いハードルを課す「とうかくうんどう♡」扱いの疑義。田中秀臣総裁も否定しないが安倍総理のポリキャピ考えたら無理筋かと twitter.com/shinchanchi/st...
タグ:
posted at 21:59:45

@genkuroki @tyoukimukou @Syance_158 指定はされていないと思います。nをうまく取らないとならなくて、そこで運が作用して、入試問題としてはどうかなと思ったのです。
タグ:
posted at 21:52:30

 非公開
非公開
タグ:
posted at xx:xx:xx

@sekibunnteisuu @tyoukimukou @Syance_158 円周率を求める問題では何か方法が指定されていたんでしたっけ?
正n角形を使えという指示があれば私も良い問題じゃないと思いますが、何でもありなら良い問題だと思います。
タグ:
posted at 21:48:50

@tyoukimukou @sekibunnteisuu @Syance_158 #数楽 あと、微積分についてはおそらく日本で最も有名な教科書である高木貞治『解析概論』には dy/dx は本物の(近似が一切ない)分数だとみなす方法が書いてあるのですが、なぜか、高校の数学の先生の中には「分数でない」と強調する人達がいるらしい。『解析概論』に目を通す気がないのか?
タグ: 数楽
posted at 21:45:36

@tyoukimukou @sekibunnteisuu @Syance_158 #数楽 高校数学の教科書の執筆陣もこの手のことを当然知っているはずなのですが、なぜか、伝統的に採用されている sin θ を挟み撃ちをする遠回りの「証明」が教科書には載っている。
伝統は崩せないということなのか?何か大人の事情があるのかもしれませんね。
タグ: 数楽
posted at 21:43:34

@tyoukimukou @sekibunnteisuu @Syance_158 #数楽 単位円弧の長さ(ラジアン)を表わす積分 θ=∫_0^y dt/√(1-t^2) の被積分函数の分母を√((1-t^2)(1-k^2t^2)) にパラメーターkの分だけ一般化すれば、楕円積分が得られ、その逆函数はJacobiのsn函数です。楕円函数論がすぐにできる。数学をやっていたら、当然知っておくべき教養の一つ。
タグ: 数楽
posted at 21:42:08

@tyoukimukou @Syance_158 @genkuroki 個人的にはあの問題、入試問題として良問かどうかは疑問です。ぱっと見て、正n角形で挟むのは思いついても、nをいくつに設定すべきか、小さいと精度が荒くなる、大きいと計算が複雑になる、で最初からちょうどいいnを設定できるかどうかは勘と運になりかねない。時間が十分にあればいいけど。
タグ:
posted at 21:39:57

@tyoukimukou @sekibunnteisuu @Syance_158 #数楽 y=sin θ の高校数学における定義は、高校数学IIIにおける曲線の長さが速さの積分で書けることを使えば、θ=∫_0^y dt/√(1-t^2) の逆函数であることが(速さを求める)ちょっとした計算でわかります。これを知っていれば、sin θの導函数がすぐに求まる。ほぼ自明。
タグ: 数楽
posted at 21:39:49

@tyoukimukou @sekibunnteisuu @Syance_158 #数楽 私は、高校数学教科書における lim_{x→0}(sin x)/x = 1 の「証明」の方針にかなり不満を持っています。三角函数の定義と逆函数の微分に関する結果か自明なのに、自明じゃないことをして、論理的にクリアでなく、ものすごく遠回りの議論になってしまっている。
タグ: 数楽
posted at 21:37:07

 非公開
非公開
タグ:
posted at xx:xx:xx

@Syance_158 @genkuroki @tyoukimukou 重要なのは定理や公式をきちんと理解することであって、それらが高校数学のカリキュラムの範囲内かどうかは重要ではない。
0以上の整数nに関する命題を数学的帰納法で証明していいのか?
高校数学の教科書では、nが1以上の整数の場合しか扱ってない。でも理解していれば0以上でも同じ事だと分かる
タグ:
posted at 21:34:56

 非公開
非公開
タグ:
posted at xx:xx:xx


@Syance_158 @genkuroki @tyoukimukou 昔東大で、加法定理を証明せよ、という問題が出たけど正答率はどの程度だったのかな?
加法定理自体は高校数学のカリキュラムの範囲内だけど、当然、「加法定理から明らか」じゃ駄目。
タグ:
posted at 21:32:31


@Syance_158 @genkuroki @tyoukimukou 指数関数や対数関数の微分を、定義に立ち返って証明するとか、高校生のほとんどは全滅じゃないかな?
タグ:
posted at 21:30:18

ほう、岩波「科学」はクズ雑誌に成り果てたので目次も見てなかったのですが、Doctor of Osteopathyなんて名乗っている人に記事を書かせていたのですか。「ニセ医療」じゃん。もう「科学」を名乗るのはやめればいいのに。同じ特集に執筆した「科学者」はそれで納得してるんですかね
タグ:
posted at 21:29:51

#統計 #JuliaLang 以下のリンク先はどちらも同じJupyter notebook
gist.github.com/genkuroki/6440...
nbviewer.jupyter.org/gist/genkuroki...
PIAACデータの解析に関する話題について
最小二乗法をしまくる話
あえて、最も単純な最小二乗法の組み合わせしか本質的に使わずに、どのような様子になっているか見てみました。
posted at 21:28:07

@genkuroki @tyoukimukou @sekibunnteisuu 今まさに曖昧な情報に騙されそうになっていますが、その点はご安心下さい
少なくとも、自らに必要な情報の取捨選択はしっかりと行っているので
タグ:
posted at 21:28:03

 非公開
非公開
タグ:
posted at xx:xx:xx

@Miyu_oekaki_315 @jh_a7 @ichiko71853 @musizudash0801 @YONI_IMIJIKI00 いきなり&横からで失礼します。
【なんで倒しちゃダメなのか・・・教えてもらいたいですよ】
という事なので、「#掛算 の順序は片方だけが正しい」という側は丁寧に教えているのだという情報をどうぞ。(私は「どっちでも良い」派ですが。)
www.asahi.com/edu/student/te...
タグ:
posted at 21:21:08

@Syance_158 @tyoukimukou @sekibunnteisuu 私が真に数学を理解しているかどうかを問うときにする質問の話をしています。
いずれにせよ、デマに騙されていたという事実を認めて反省することは大事なことだと思いました。失うものが多過ぎ。受験やら数学やらの話ですまない。デマに騙される自分を認めることができるかどうかという問題。
タグ:
posted at 21:19:05

#統計 例えば、最近話題になっていた
kivantium.hateblo.jp/entry/2017/11/...
の推定結果は、国別に分けての最小二乗法でa[i],b[i](および残差の標準偏差)を求めた後に、a[i],b[i]それぞれの平均・標準偏差を求めた結果とほぼ同じになります。
国別に分けて最小二乗法を実行する計算は一瞬で終わる。
タグ: 統計
posted at 21:11:58

@genkuroki @tyoukimukou @sekibunnteisuu 大学受験で受験生がほぼ全滅する問題って、複雑な計算の問題ならともかく、そういう理解度を問う類いの問題では聞いたことが無いのですが、一体どんな人が受ける大学ですかね……
とりあえず「正しければ何でも良い」っていう輩にも注意しておくようにしておきます
タグ:
posted at 21:09:55





 非公開
非公開
タグ:
posted at xx:xx:xx

 非公開
非公開
タグ:
posted at xx:xx:xx

@Syance_158 @tyoukimukou @sekibunnteisuu 「〇〇しか使っちゃいけない」とか言う数学の先生はレベルが低いので本当に注意した方がよいと思います。そういう輩に従うと不合理で不自然な議論の仕方を身に付けてしまいます。
タグ:
posted at 20:53:35

@Syance_158 @tyoukimukou @sekibunnteisuu 正確な議論と正確な計算を理解抜きに行うことは困難です。
「使ってよい事柄の範囲内でなんとかする計算ゲーム」の類として数学を習得しようとすると、低レベルな数学の理解になる可能性が高いです。
それは受験以前に論外でしょう。
数学的に自然な議論を避けることは効率が悪く、理解を妨げます。
タグ:
posted at 20:52:00

@Syance_158 @tyoukimukou @sekibunnteisuu そういう残念な現実の中で、相当に理解度が高い人たちもいて、そういう人達の答案は整然としていて、議論が正確(例えば場合分けを漏らしていたりしない)で、計算も正確だったりします。そういう基礎能力を鍛えることを優先するべきで、くだらないこと(〇〇は使ってはいけないなど)は忘れた方が得です。
タグ:
posted at 20:48:49

@Syance_158 @tyoukimukou @sekibunnteisuu 学習指導要領内のことがらであっても、高校生に理解しているかどうかを問う質問をきちんとすれば、ほぼ全滅に近い状態になると思います。教科書も結構ひどい。これが残念な現実です。
大学の数学の先生は「高校で教わっていることの証明を高校生が理解している」と思っていないという現実を見るべき。
タグ:
posted at 20:46:37

@tyoukimukou @Syance_158 @sekibunnteisuu 学習指導要領内の事柄であっても証明を理解せずに使っている受験生がいることを採点者たちは知っています。証明云々は学習指導要領云々とは無関係の問題です。
「学校で習ったから理解していると推定できる」という発想は数学の採点では非現実的。その程度のことは小学生も多分理解できると思う。
タグ:
posted at 20:41:27

@Zi_kade @sekibunnteisuu 私が保護者なら子供が2年の時点で
「#掛算 の順序は片方だけが正しいとは理不尽な。
だが仕方ない、学校で教わった通りにやりなさい」
と教え、単位の換算は 1000×3 だと教えるでしょう。
そして上の学年に行った時先生が「3×1000」と言ったら
「2年生の時のは何だったのか!」と怒るでしょうね。
タグ:
posted at 20:40:56

@tyoukimukou @genkuroki @sekibunnteisuu 本当に「正しければ何でもアリ」なら、その道中の計算式に間違いが無ければ「正しい」物です
というか最悪、正しい値さえ出せば大丈夫でしょう
ただの計算ゲームと化しますけど
そこで理解を示すために文章を書き、使う事が可能な事実のみを使って説明する事が数学において大切だと僕は考えます
タグ:
posted at 20:39:35

 非公開
非公開
タグ:
posted at xx:xx:xx







@genkuroki @tyoukimukou @sekibunnteisuu 「証明済みの事実」から「証明されていない命題」を証明しなくてはならない
という面では「縛りがある状態」で解かないとそれこそ数学的な実力は上がらないかと……
あと、正しければ何でもアリなんて道中の計算式を羅列しただけで満点が貰える世界、是非行きたいですね
タグ:
posted at 20:20:54


#統計 「頻度主義 vs. ベイズ主義」というおかしな対立図式をフルボッコにし、最尤法とベイズ推定法を情報量規準(汎化損失の推定量も情報量規準の一種)という同じ視点から眺めて理解することは、40年近く前にすでに赤池弘次さんがやっていたことです。
twitter.com/genkuroki/stat...
タグ: 統計
posted at 20:13:40


#統計 #JuliaLang 最尤法やベイズ推定法による推定結果はどちらも予測分布(サンプルを生成している未知の確率分布の推定結果)になります。予測分布の予測誤差の大きさはKullback-Leibler情報量で定義される。しかし、KL情報量自身をサンプルだけから計算することはできません。続く
posted at 20:06:54

#統計 #JuliaLang 上で紹介した動画を見れば、確率モデルを設定してのベイズ推定がどのようにサンプルを生成している未知の分布を推定することになるかについて、明瞭なイメージがつかめると思います。
採用した確率モデルの範囲内でサンプルを生成している未知の分布に推定結果は近付く。
posted at 20:05:01

#統計 #JuliaLang 以上で紹介した動画は、Julia言語のMambaパッケージを使ったMCMCによるベイズ推定の結果なのですが、同じモデルで最尤法を使った推定をしてもほぼ同じ動画が得られるはずです。今回扱ったケースはどれも正則モデルを扱っているとみなしてよさそうなので。
posted at 20:03:37

#統計 #JuliaLang 確率分布を決めるパラメーターよりも、確率分布そのものの方が本体です。本体を見るのを止めて、本体の属性に過ぎないパラメーターだけに注目するから色々おかしな考え方をしてしまうのだと思う。
未知の確率分布を推定する方法として、ベイズ推定法と最尤法は完全に仲間。
posted at 20:02:11

#統計 #JuliaLang ベイズ統計に関する俗流の解説の多くは、確率モデルのパラメーター空間上の事前分布と事後分布を中心に扱うようですが、個人的にそういう解説の仕方はよくないと思う。
「ベイズ推定も最尤法もどちらも未知の確率分布を推定する方法である」という立場の方がすっきりしている。
posted at 20:00:01

#統計 #JuliaLang 分散1の山が2つの混合ガンマ分布を分散1の山が2つの混合正規分布でベイズ推定。これはかなりフィットしている。サンプルサイズが増えるにしたがって、左側の小さな山を混合正規分布モデルさんが認識して行くようになる様子が見えます。 pic.twitter.com/sxhi0lZBDr
posted at 19:58:19

#統計 #JuliaLang 分散1のガンマ分布の山が2つの混合ガンマ分布を1つ山の分散1の正規分布でベイズ推定。さすがにこれはきつい。全然フィット感がない。 pic.twitter.com/07u2Z3NCz8
posted at 19:55:25

#統計 #JuliaLang 分散1のガンマ分布の山が2つの混合ガンマ分布を1つ山の正規分布でベイズ推定。ベイズ推定の収束先は推定に使った確率モデルに含まれる確率分布でサンプルを生成している確率分布に最も近いものになります。 pic.twitter.com/PMSc4NqoDt
posted at 19:54:21

#統計 #JuliaLang 分散を1に固定した2つ山の混合正規分布モデルで1つ山のガンマ分布にフィッティング。フィッティング先が1つ山なのであんまり面白くないですが、やはりKL情報量(予測分布の予測誤差)が0.05強まで下がっています。 pic.twitter.com/O0965wso3u
posted at 19:52:28

#統計 #JuliaLang サンプルを生成したガンマ分布の分散も1にしてある。分散を1に固定した正規分布でフィッティングすると、分散を固定していない場合よりも速やかにKL情報量が減少します。パラメーター数が少ない方が収束が速くなります。 pic.twitter.com/efVbsvGBag
posted at 19:47:08

#統計 #JuliaLang 18個のGIF動画を作りました。添付動画はそのうちの一つ。正規分布にちょっと近いガンマ分布をベイズ推定で正規分布でフィッティングしています。サンプルの中身を1個ずつ増やして推定を繰り返しています。KL情報量が速やかに下がっている。0.05強の下限がある。 pic.twitter.com/t66ZQgWkx4
posted at 19:45:14

#統計 #JuliaLang 続き
mixnormal=分散1の正規分布が2つの混合正規分布モデル(パラメーターは3つ)。
2. θ_1=0.4, θ_2=0.18に対する2つ山の混合ガンマ分布モデル 0.3Γ(1/θ_1^2,θ_1)+0.7Γ(1/θ_2^2,θ_2) でサンプルを生成して、1と同じことをする。
posted at 19:42:45

#統計 #JuliaLang 何をやったか
1. θ=0.4に対するΓ(1/θ^2,θ)分布でサンプルを生成。サンプルの中身を1個ずつ増やしながら、以下の3つのモデルで推定。
normal=パラメーターが平均と分散の2つの正規分布モデル
normal1=分散を1に固定した平均だけがパラメーターの正規分布モデル
続く
posted at 19:39:13

@Zi_kade @sekibunnteisuu なお、「並べ替え」とは
「ABCDの4枚のカードを1列に並べる並べ方は、何通りか?」という問題です。
この件は積分定数氏に任せます。 #掛算
タグ: 掛算
posted at 19:36:41

#統計 #JuliaLang
genkuroki.github.io/documents/Jupy...
でベイズ推定のGIF動画を作るための Jupyter notebooks と作ったデータファイルがすべて公開されています。
posted at 19:35:37


#統計 #JuliaLang サンプルサイズを1ずつ増やして、ベイズ推定して得た予測分布の形がどのように変化して行くかを見るためのGIF動画を作成しました。動画の実例については
genkuroki.github.io/documents/Jupy...
と
genkuroki.github.io/documents/Jupy...
の最後の節を見て下さい。
posted at 19:34:30

【順序固定派はパターンマッチングしている場合が多く、暗記パターンから外れる複雑な問題では順序が分からなくなる】
それはありそうですね。 #掛算 twitter.com/LimgTW/status/...
タグ: 掛算
posted at 19:28:23

@Zi_kade @sekibunnteisuu 【単位の換算は3×1000でも逆1000×3でも】
横からで失礼します。
単位の換算では
「1000 という塊が 3つある、だから 1000×3 のみが正しい」という話になるのかと思っていたのですが、そうではないのですか? #掛算
タグ: 掛算
posted at 19:25:58

@tyoukimukou @Syance_158 @sekibunnteisuu ポイントは数学的な実力そのもの。
おかしな勉強の仕方(〇〇しか使ってはいけないと縛りがありまくりの勉強の仕方)をすると、数学的な実力が低くなり、結果的に受験数学の問題も解き難くなり、点数が下がって一方的に損をしてしまうと思います。
本物の数学の実力を身に付ける勉強をして下さい。
タグ:
posted at 19:12:32

@tyoukimukou @Syance_158 @sekibunnteisuu ある人は大学の数学先生の目から見て数学的に正しい答案を書けば何でもありだと思って受験の準備をする。
ある人は先生が使ってよいと言ったことだけしか使っちゃいけないという前提で受験の準備をする。
数学の実力に大きな差がつくように思えます。
デマに惑わされると損をします。
タグ:
posted at 19:07:47

@tyoukimukou @Syance_158 @sekibunnteisuu 学内でも、「大学受験生は高校生だけじゃないですよね」という話をすると同僚もきちんと「うん、うん」とうなずいてくれます。
私は学問的に真っ当な人達に囲まれて仕事をしていることを誇りに思っています。
ここまで言っても信用しないなら自己責任。大学受験では一方的に損をすると思います。
タグ:
posted at 19:05:48

@tyoukimukou @Syance_158 @sekibunnteisuu まあ、数学的に有害な採点をする高校の数学の先生はきちんと社会的に非難されてしかるべきであることは確実。
数学の基本は正しければ何でもありです。
そして、理解している人の答案は数学的な道具として何を使っていても理解していることがわかるようにきちんと文章が書かれているものです。
タグ:
posted at 19:02:27

 非公開
非公開
タグ:
posted at xx:xx:xx

@genkuroki @sekibunnteisuu それは黒木さんが「証明済み」だと理解しているからこその採点だと思います
数学において証明済みか否かは最重要項目ですし、どこまでを「証明済みなので証明不要」とするかの線引きを明確にする必要があると僕は考えてます
そこが曖昧なので、このような問題が発生してしまっているのではないかと
タグ:
posted at 18:36:55


@genkuroki @sekibunnteisuu 採点者によってブレが生じる事は知っていますし、だからこそ学習指導要領に沿って「誰が採点しても満点が得られる答案」を作るのが残念ながら「受験」という物です。
ただ、個人的には「学習指導要領」は「既に教員が代わりに証明した事」だと認識しているので、その範囲外を使うのは気が引けます……
タグ:
posted at 18:28:08

@Syance_158 @sekibunnteisuu 変な採点基準で数学の試験を採点している先生達は受験生にとって有害な存在です。もちろん数学の正常な理解という観点から見ても極めて有害。
そのような数学教師は若い人達を惑わす社会的に有害な存在なので、何らかの形で是正されることが望ましいと思っています。
タグ:
posted at 18:24:26

@Syance_158 @sekibunnteisuu 大学受験生は高校生だけではありません。
数学的に常識ある人が採点しているなら、「数学的に正しいか否か」「数学的に合理的であるか否か」などの基準で採点し、学習指導要領の内容は完全に無視するはずです。
デマに惑わされたまま大学受験しないように気を付けて下さい。
タグ:
posted at 18:21:44

メルカリで3か月以上売れなかった英語の本、カテゴリを書籍からインテリア雑貨に変えたら5時間後に売れた・・使い方の提案次第でこんなに違いが出るのは面白いなあ
タグ:
posted at 17:42:03

@sekibunnteisuu 現在進行形で受験生なので、それによる減点を何度も喰らったことがあります。(特に数Ⅲ積分の範囲で)
「習っていない事」
とは、教師によって
「証明されていない事」
に等しいです。
言い方をそちらに変えれば「大前提」になっているとご理解頂けるでしょうか……?
タグ:
posted at 17:38:11

@Syance_158 「大前提」からずいぶん後退したように思えますが・・・
また、「少なくとも受験数学界においては学習指導要領の範囲外の方法を使うと減点(場合によっては不正解)される危険性があります」というのは根拠はあるのでしょうか?
タグ:
posted at 17:29:02

@sekibunnteisuu 少なくとも受験数学界においては学習指導要領の範囲外の方法を使うと減点(場合によっては不正解)される危険性があります
教員が教えていない物は、例え正しく理解しても「その教育機関内では」存在していないに等しいので、使わない方が良いかと。
タグ:
posted at 17:25:36


はてなブログに投稿しました #はてなブログ
Rで名刺 ggplot2編 - まだ厨二病
uribo.hatenablog.com/entry/2017/11/...
タグ: はてなブログ
posted at 15:29:08



 非公開
非公開
タグ:
posted at xx:xx:xx


 非公開
非公開
タグ:
posted at xx:xx:xx

 非公開
非公開
タグ:
posted at xx:xx:xx

明日の国際会議の発表。僕の講演テーマが「phase transition out of equilibrium」なので、40年前の風景から入ることにした。動的臨界現象が確立し、散逸構造に関する本が出版され、蔵本モデルが提案された。(さて、この流れで、今日のを1枚追加するかどうか。) pic.twitter.com/iZTmbppZen
タグ:
posted at 10:54:19

 非公開
非公開
タグ:
posted at xx:xx:xx

 非公開
非公開
タグ:
posted at xx:xx:xx

Kouji Ohnishi 大西浩次 @koujiohnishi
第11話の黒板の数式は、蔵本モデルの同期現象の”相転移”! twitter.com/Perfect_Inside...
タグ:
posted at 10:25:19

Kouji Ohnishi 大西浩次 @koujiohnishi
第11話の黒板の数式は、蔵本モデルの同期現象の”相転移”! twitter.com/Perfect_Inside...
タグ:
posted at 10:25:04

Kouji Ohnishi 大西浩次 @koujiohnishi
#仮面ライダービルド
第11話の黒板の数式は、蔵本モデルの同期現象の”相転移”! twitter.com/tonagai/status...
タグ: 仮面ライダービルド
posted at 10:24:03


#仮面ライダービルド 第11話の黒板の数式は、蔵本モデルの同期現象の”相転移”! sci.tea-nifty.com/blog/2017/11/p... pic.twitter.com/4v9l5Ywm4f
タグ: 仮面ライダービルド
posted at 09:36:41

@sekibunnteisuu @golgo_sardine ありがとうございます。
ちなみにですが、=で帯分数をつなげたら×をされたそうですが、
これは=でつなげてはいけないのでしょうか?
タグ:
posted at 09:21:30

かけ算の順序問題(逆にしたら不正解扱い)なんてのがあるのか。個人的には順序逆でも良いように思うが。そもそも私は子供のころ,九九を半分しか覚えなかった。7×4は頭の中で,覚えてる方の4×7と読み直してたなぁ(今もそうかな…)。
タグ:
posted at 08:48:36

@moukaricom @golgo_sardine これは先生が模範解答の見方を誤っているのでしょうね。
括弧は「別解」という意味で、「こっちでもいいよ」という意味に解釈するのが普通です。
タグ:
posted at 07:34:41

世界の農耕地の分布を30mという高い解像度で明らかにした地図を米国地質調査所が制作。縮尺と表示場所が可変のオンライン版が公開された。 bit.ly/2zfxaq5 たとえば関東にズームインすると興味深いパターンがみられる。世界的な人口の増加に対応した食料生産のための資料として整備された。 pic.twitter.com/4Mwfau4xJ7
タグ:
posted at 07:34:24

自殺は(安倍政権以前からの傾向ですが)、ずっと下がり続けていますよ。
働きたくても職の無かった人が多く就労し、若者の就職状況も大幅に改善し、子供の貧困状況も改善が見られております。
twitter.com/takemuraakihir...
タグ:
posted at 03:18:45

具体的にどこの何がどう嘘なのか指摘していただけると有り難いです。
twitter.com/okura_yamakawa...
twitter.com/okura_yamakawa...
タグ:
posted at 03:14:42

「確定値」で私が何か主張を変えなくてはならないような変化があったのなら、具体的に(←ここ大事)何がどう変わったのか教えて下さい。
twitter.com/hi_sunrise07/s...
タグ:
posted at 03:11:39

2008年の第四四半期に、飛び上がってます。
その後に、報酬が大幅に下がった。
www.chusho.meti.go.jp/pamflet/hakusy... pic.twitter.com/efzF0vSpP6
タグ:
posted at 02:52:31

いまだにこんな 鹿。 みたいなことを言っている人が多い事に驚きます。
「アベノミクスによろしく」みたいなアホ本には書いてないかも知れないが(読んでない)、デフレはまず実質賃金の上昇をもたらすという事は、ちょっと調べれば分かること。
twitter.com/ishtarist/stat...
タグ:
posted at 02:46:58
なかなか凄い発言。
ノートの種類をわざわざ強制している。普通の大学ノートや無地ノートのほうが好きな子はどうなるのか。そもそもノート自体自分のために好きなように取るもので、授業を聞くだけで覚えられるなら書く必要もない。プリントの裏や教科書の余白に書き込んだっていい。 twitter.com/ussiarmoakluma...
タグ:
posted at 00:10:01



