黒木玄 Gen Kuroki
- いいね数 389,756/311,170
- フォロー 995 フォロワー 14,556 ツイート 293,980
- 現在地 (^-^)/
- Web https://genkuroki.github.io/documents/
- 自己紹介 私については https://twilog.org/genkuroki と https://genkuroki.github.io と https://github.com/genkuroki と https://github.com/genkuroki/public を見て下さい。
2019年11月10日(日)


英語民間試験は専門家の意見を無視したために破綻しました。その部分を反省して専門家に意見に従い「改革」を断念したという形を作らなければいけません。そうしないと,またいつ覆されるか分かりません。
これが,僕が専門家の方々に声を挙げて戴きたい理由です。
タグ:
posted at 23:49:19

阿部公彦 ABE Masahiko @jumping5555
「週刊文春」がこのスクープをやったのが2015年4月。英語民間試験が不透明なプロセスをへて導入されることに決まったのは2016年から2017年にかけて。記事の時点で「膿」をだしておけば、今の混乱はなかった。今回こそはきちんと治療して「膿」を出さないと、また数年後同じことが起きますよ。 pic.twitter.com/EQHlk71ZFZ
タグ:
posted at 23:08:40


Sheaf@ピアノアルバム2枚配信中 @Kanata_journey
今日の数学シェーダー。
neort.io/art/bn40hks3p9...
www.shadertoy.com/view/tdyXzh
複素数の累乗を実装(というほどのものでもないが)して、100次方程式(ほとんどの係数は0)の解の分布を視覚化した。
やっぱり、複素数ってすごいわ。
#glsl #creativecoding #数学 pic.twitter.com/HvUjvWrIXK
タグ: creativecoding glsl 数学
posted at 22:04:58

 非公開
非公開
タグ:
posted at xx:xx:xx
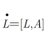
Integrable Systems, @integrablesys
Did you know that the ancient Japanese art of origami is nontrivially related to PDEs? More at rdcu.be/bWw7g @SpringerMath
@adhara_mathphys @chibafx @emulenews @genkuroki @hfymd @Paul_Painleve @ta_to_co @7shi
Free to read link 🔼 made using HT ▶️ twitter.com/OpenScienceR/s... pic.twitter.com/PIYkb5DhLB
タグ:
posted at 21:20:32

 非公開
非公開
タグ:
posted at xx:xx:xx

YOSHIDA Hiroshi 吉田寛 @H_YOSHIDA_1973
こんなのがあるんですね。作問委員の体験記です。私の感覚ではこれは「書き過ぎ」のような気がしますが(笑)せっかく公開されているものなので、周知・拡散させていただきましょう。/「2002年センター試験問題(数学)はこうして作問された」佐藤恒雄『数学資料』48号 www.jikkyo.co.jp/download/detai... twitter.com/yearman/status...
タグ:
posted at 20:47:31

#Jupyter さらに、ノートブックを公開したURLを
nbviewer.jupyter.org
に貼り付けることによって、ノートブックをきれいに整形して閲覧でき、さらにそのノートブックがRISEでプレゼンできるようになっていれば、それでプレゼンすることも可能になります。 pic.twitter.com/9KOXBk1PYe
タグ: Jupyter
posted at 20:42:04

#Jupyter
Jupyter notebook + Nbextensions: Gist-it
を使えばノートブックをワンボタンでGitHub Gistで公開できます。 pic.twitter.com/jSB9KAFeeF
タグ: Jupyter
posted at 20:38:35

こういう文章が公刊されていますが,これよりもっと細かなこと,ですよね>2002年センター試験問題(数学)はこうして作問された www.jikkyo.co.jp/download/detai... twitter.com/H_YOSHIDA_1973...
タグ:
posted at 20:36:25

#Jupyter
さらにRISEも追加すれば、Jupyter notebookでそのままプレゼン可能です。スクショはiPad上のChrome pic.twitter.com/uMKz0cPWrF
タグ: Jupyter
posted at 20:24:10

必見。「ニセ医療を提供している医師の医師免許はなぜ安泰なのか」と思います。
自由診療について一切の規制がないことは大きな問題。
ニセ医療で一番悪いのは医師です。間違いない。仕組みとして規制するべき。
残念ながら、すぐには仕組みが変わらないから患者さんに警鐘を鳴らしているわけです。 twitter.com/nonbeepanda/st...
タグ:
posted at 19:43:26

#Jupyter
iPadOS上のChromeから、自宅Jupyterサーバーにアクセスして、Jupyter notebookでも、JupyterLabでも日本語を入力できることを確認できました。
これは結構でかい改善。
JupyterLabでディレクトリの移動もできるようになっていました。
自宅Jupyterサーバー+ZeroTier環境は結構お勧め。 pic.twitter.com/YYnHnzN4vt
タグ: Jupyter
posted at 19:36:10

岩上安身はこのデマの責任を取ったのか?反省・謝罪をしたのか?ジャーナリストとしてはとっくに終わってるよね twitter.com/kiri_7771/stat...
タグ:
posted at 19:31:19


掲示板の内容より。
【①比の比例式を区別しましょう】
「比と比例式を区別しましょう」の記載ミスですよね。
a:b は比である。
a:b=c:d としても、a:b の部分に着目すれば比である。(比と比例式を分離するような物言いには???ですね)
比例式は、比を等号で結んだだけものではないのですか?
タグ:
posted at 18:49:22

私の比に関する主張はこれだけです。
複数の数の関係を a:b のように記述出来る。
a と b は対等な関係。
同じ関係のものを a:b=c:d のように等号で結べる。
タグ:
posted at 18:49:22

ニセ科学系の元文科大臣の議員は国会から消えれば良いと思う。
大臣にニセ科学推進を勧める野党議員にも国会から消えてもらいたい。
野党側が与党側のニセ科学推進の動きを徹底殲滅しようとするのではなく、一緒に推進側に回ってしまう地獄。
タグ:
posted at 18:38:20

森ゆうこさん曰く【下村文部科学大臣も御関心のあるナノ純銀によるセシウム低減技術があります。~まずは、しかるべき機関に実情を調査研究させるべきと考えますが、下村大臣、いかがですか。】
ニセ科学に御関心のある文科大臣にニセ科学研究推進を勧めてた!地獄だな😱
twitter.com/itallmatuzaki/...
タグ:
posted at 18:30:08

良記事。記事の最後にあるように、今後は医療や健康に関する情報発信には極力慎重になっていただきたい。批判や火消しはやる方も気分の良いものではないので。批判を受けて頑なに拒絶するのではなく、耳を傾けられるよ... #NewsPicks npx.me/pdkT/TsvK?from...
タグ: NewsPicks
posted at 17:59:26



numpy.random.choice
(ある確率分布:weight に従って、keyを選択する)
をJuliaで実現するには、StatsBaseのsampleを使用すれば良い
#Julialang pic.twitter.com/wbZTQV2s4c
タグ: Julialang
posted at 16:48:27

@MathSorcerer @genkuroki ありがとうございます。Apollonian gasket の円の数が不正問題をどうにかしてから、他のいくつかのフラクタルの実装とまとめて記事を書こうと思います。
タグ:
posted at 16:28:29

ごまふあざらし(GomahuAzaras @MathSorcerer
@triwave33 懺悔するとレコーディング中「あ,Julia負けるな・・・」って思ってました.
タグ:
posted at 15:45:50

ごまふあざらし(GomahuAzaras @MathSorcerer
@physics303 ターゲットにする分野にもよると思います.(画像処理系などはまだまだやるべきことが多い)
タグ:
posted at 15:45:01

Nobu Kagiyama@Heart @KagiyamaNobu
@atmizu @mph_for_doctors @Shuntarooo3 なんかデータはありましたが、明らかに医学統計ではR増えてますしね。一流紙も含めて。
タグ:
posted at 15:44:52

Nobu Kagiyama@Heart @KagiyamaNobu
@atmizu @mph_for_doctors @Shuntarooo3 やっぱ基本医学統計はまだ全然Rのが楽と思います。tidyverse神がいるし。
ただしRはpythonに、pythonはRに似た処理ができるパッケージがどんどん増えているので、違いは小さくなってきていると聞きますー。
タグ:
posted at 15:43:36

ごまふあざらし(GomahuAzaras @MathSorcerer
本当はPythonだけ,Juilaだけで動かすとか JuliaはREPL立ち上げて動くこと前提としてるので立ち上げた段階から始めるべきなどはありまふがエンタメ要素としては楽しかった
タグ:
posted at 15:38:02

ごまふあざらし(GomahuAzaras @MathSorcerer
maxdepth=5 でのギリギリの戦いをご覧ください. pic.twitter.com/ijV15RgrLE
タグ:
posted at 15:33:22

ネメシスの悪事を記録するkiriナントカ @kiri_7771
岩上安身のデマ「(常磐道開通を受けて)車両を通じて汚染が列島中にじわじわと拡散」 - Togetter togetter.com/li/634404 @togetter_jpさんから
タグ:
posted at 15:05:19

#統計 分割表の独立性検定で使うχ²分布の自由度については、Fisher-Pearson論争が有名で、Fisherの1922年の論文は無料で読める。
Fisherさんは「縦横の合計を全て固定する」という正しい答えは出るが理屈的には間違っている議論で正しい自由度を求めてしまっています。
twitter.com/genkuroki/stat...
タグ: 統計
posted at 14:47:41

#統計 誤りが書いてある本の例
粕谷英一著『生物学を学ぶ人のための 統計の話~きみにも出せる有意差~』文一総合出版1998
実際には、縦横の合計を固定しない現実的な想定においては、Fisher検定による近似の誤差はχ²検定よりも非常に大きくなる傾向があります。 pic.twitter.com/oNwO8qkr4V
タグ: 統計
posted at 14:38:43

ごまふあざらし(GomahuAzaras @MathSorcerer
左がJuliaで右がPythonね twitter.com/MathSorcerer/s...
タグ:
posted at 14:36:34

ごまふあざらし(GomahuAzaras @MathSorcerer
@physics303 @genkuroki depth=6 での終了目安時間(ETA)にご注目 pic.twitter.com/FpkYWr2EcS
タグ:
posted at 14:33:46

ごまふあざらし(GomahuAzaras @MathSorcerer
@physics303 @genkuroki JuliaとPythonの自分のスクリプトを同時に走らせてるけれどJuliaは起動のオーバヘッドのハンデがあっても最終的にJuliaが勝つ
タグ:
posted at 14:28:37



ごまふあざらし(GomahuAzaras @MathSorcerer
@physics303 @genkuroki そしてそろそろ,元実装で参考にした自然言語で書かれている Referenceが何だろうかが気になってきた(Qiita楽しみにしてるでkyu!!)
タグ:
posted at 14:15:13


ごまふあざらし(GomahuAzaras @MathSorcerer
@physics303 @genkuroki 慣れの問題もあってPythonの方はすぐ実装できたし generator の実装もスマートにできるけれど,それ以外のことで実装上発生する問題を回避する方法はJuliaの方がやりやすい.
タグ:
posted at 14:14:16


ごまふあざらし(GomahuAzaras @MathSorcerer
Yet Another Python implementation
gist.github.com/terasakisatosh...
Cc: @physics303 @genkuroki pic.twitter.com/IKRBhZMF3j
タグ:
posted at 14:06:27

#統計 分割表
1 2
5 0
の独立性検定において、想定する可能な分割表の種類の個数は、Fisher検定が前提にする縦横の合計を全て固定する超幾何分布の場合にはたったの3個ですが、
横の合計3,5のみを固定する場合→24個
全合計8のみを固定する場合→165個
制限無し→∞個
twitter.com/genkuroki/stat...
タグ: 統計
posted at 14:02:34

悪質なデマを飛ばしていたのは森ゆうこ議員です。
「デマとはもう付き合いたくない」というなら、自分のデマをしっかり反省すべきです。 twitter.com/itallmatuzaki/...
タグ:
posted at 13:43:26

#統計 Yatesさんの1984年の論文のpdfの外でその論文がどのように評価されているか?その例↓
people.stat.sc.edu/Hitchcock/yate...
Yates and Contingency Tables: 75 Years Later
David B. Hitchcock
2009
2009年の段階でYatesさんに対する致命的な誤解の指摘のダメージは皆無だったようです。 pic.twitter.com/I5Xtsf3MIw
タグ: 統計
posted at 13:06:59



#統計 Yatesさんの1984年の論文のpdf
mathfaculty.fullerton.edu/sbehseta/Yates...
には他の専門家たちによるコメントも収録されており、私が指摘したYatesさんの致命的な誤解もしっかり指摘されています。 pic.twitter.com/VHaSvPsKAA
タグ: 統計
posted at 12:38:29



自分でも宣伝。『機動警察パトレイバー 』愛蔵版、発売されました。おそらくこれが作者生存中最後の『パトレイバー 』単行本になります(笑)。値段が若干お高いですが、函入り造本、カラーページも復刻されておりますので、お財布にゆとりがありましたら、是非お手に取っていただけると幸いです。 pic.twitter.com/hTIykV4LFI
タグ:
posted at 12:10:23


#統計 決定的だと感じたこと。Yates補正のYatesさんの1984年の論文を見たら、Yatesさんは、独立性のχ²検定もまたFisher検定と同様に縦横の合計を固定しなければ意味を持たない検定(conditional test)だと誤解していた!!!
これは致命的。言い訳不可能。
mathfaculty.fullerton.edu/sbehseta/Yates... pic.twitter.com/746LqZZMmV
タグ: 統計
posted at 12:04:13


ごまふあざらし(GomahuAzaras @MathSorcerer
@triwave33 頻繁にJulia ,Python間を細かくやり取りしてで速度が要請される物は厳しいかもですねー.どっちかの言語で書いたまとまったコードを呼び出すというシチュエーションではいいとおもいます.
タグ:
posted at 11:58:12





 非公開
非公開
タグ:
posted at xx:xx:xx




@atmizu @Shuntarooo3 あっ、医学統計は圧倒的にRがいいと思います。
Pythonだと信頼区間ひとつ求めるのも一苦労です(Bootstrap除く)。
タグ:
posted at 11:14:02

@mph_for_doctors @Shuntarooo3 やはり、、、、
ちょっと医学統計はRと信じてたのに、、、
そういう感想がチラホラきていると感じてます!
タグ:
posted at 11:12:49








Sato Shuntaro|佐藤俊太朗 @Shuntarooo3
@atmizu 機械学習ではpythonが一般的になっていると思いますし、Juliaという言語もちらほら目にするようになってきましたが、統計ユーザーへの浸透はRもまだまだこれからだと思いますよ!
再現性を担保したデータ解析がマストになってくると一気にR使用者増えると思います😀
タグ:
posted at 10:44:38
#はてなブログ
ブランシャールのMMT論 - himaginary’s diary
himaginary.hatenablog.com/entry/20191109...
タグ: はてなブログ
posted at 09:53:42


同時に,それでも懲りずにオープンな議論抜きに,1次どころか2次試験にまで民間試験を持ち込もうとする勢力があるのが情けない。今度こそ,メディアや(与野党問わず)心ある政治家に見張っていていただきたい。大臣の失言が続くまで動いてくださらなかった今回の反省に立って。
タグ:
posted at 08:40:21

1年以上前の高校生とのやり取りにイイネをしてくださる方がいた。読み返すと,制度が破綻し選抜が不成立になるようなことがあってから止まるよりは,事前に止めることができてまだ良かったと思う。→ twitter.com/KITspeakee/sta...
タグ:
posted at 08:31:18

藤原 康弘 | Fujiwara Yas @yasuhiro008
寺沢さん:この「日本の英語力は××位!○○共和国は××位!(以下略)」という話は、ほとんどの場合、信頼がおけないデータに基づいているので騙されてはいけません。1/2
「日本の英語力は53位」というデマ報道が流れ出す季節になりましたね。(寺沢拓敬)
news.yahoo.co.jp/byline/terasaw...
タグ:
posted at 07:06:15
実験グループの人にJuliaで書かれた簡単な解析コードを送って、向こうはmatlabに書き直して使ったりしてたらしいんだけど、Juliaはmatlabよりとても早いね、というメールが来てて、やった!という感じ
タグ:
posted at 06:44:49

#統計 添付画像右下のプロットはFisher検定の基礎である超幾何分布(周辺度数固定)でサンプルを生成する設定でのプロットです。離散性の影響が他の3つの場合(周辺度数は固定されない)と比較すると圧倒的に強い。 pic.twitter.com/z3nGieFwW7
タグ: 統計
posted at 04:51:45








ごまふあざらし(GomahuAzaras @MathSorcerer
深さ7にしてできた様子.かっこいい twitter.com/MathSorcerer/s... pic.twitter.com/0Edtk0XRb6
タグ:
posted at 00:59:55

This slow motion video depicts the motion of the brain during an impact event. Concussions are the most common form of traumatic brain injury & are a growing concern in many contact sports [Source, University of California: ow.ly/3z0N30nOnGn] [more: ow.ly/MnvP30nOnGV] pic.twitter.com/XhuUfZcXUd
タグ:
posted at 00:39:22






