黒木玄 Gen Kuroki(@genkuroki)/2021年03月/Page 17

出典
国民文庫編集委員会監訳(著者はレーニン及びスターリンだが奥付に書いてない)「党建設の基本問題」国民文庫、1954年 pic.twitter.com/SCStVNsK5i

タグ：

posted at 00:10:22

Jacob Quinn @quinn_jacobd

Not a bad idea at all for managing python envs. Super happy with #JuliaLang's modern builtin package manager + environments + "automatic" binary dependency management systems that all make things Just Work. twitter.com/svpino/status/...

タグ： JuliaLang

posted at 01:52:10

Ari Katz @akatzzzzz

@UQprofessional @beckness For the kind of stuff you do, python wouldn't provide enough of a marginal benefit. Julia much better for custom analyses, playing around with distributions, AD etc

Check this out github.com/AnderGray/Prob...

タグ：

posted at 02:30:44

匿本名太郎 @kaisekigakumoyo

フロベニウスノルムだと次元分の定数が出てくることがあって，なにか損をした気分にならないこともない．どっちでもいいのだけれど後で変えるのが面倒．

タグ：

posted at 05:28:53

Kaz Muzik @kazmuzik

伊賀公一世界は変えられる１人が1度 @iga6

CUDA.jlをインストールしてみた。github.com/JuliaGPU/CUDA.jl CUDA111, CUDNN_CUDA111, CUTENSOR_CUDA111がダウンロードされ、CUDA 11.1.0関連のライブラリなどがインストールされた。RTX 2080 Tiも無事に認識された。TutorialsのInstruction juliagpu.github.io/CUDA.jl/stable... を見て、BenchmarkToolsも‥ pic.twitter.com/Vguxs8NE8c

タグ：

posted at 05:53:31

Ｐ型Ｄ型の色覚には難攻不落というかあっという間に終了してしまうのでルールもわからなかったというほどの「ぷよぷよ」が、多様な色覚に対応したのをお披露目するのに、CUD友の会でオンライン開催した時の話がニュースになりました。私もコメントしてます。

game.asahi.com/article/142571...

タグ：

posted at 07:14:39

@kaityo256 #数楽確率変数Xについてf(X)の期待値とXの期待値でのfの値の違いの話は、本質的にJensenの不等式の話題になります。

その証明の中身を見れば、f(X)の期待値とf(Xの期待値)の違いが、y=f(x)とそのx=(Xの期待値)における接線の違いから来ていることが分かります。こういうイメージの仕方は結構大事。 pic.twitter.com/6UkLFj5mk6

タグ：数楽

posted at 07:22:51

#Julia言語 #数楽 Kuramoto model には相互作用の強さを表すパラメータKが入っていて、Kがある値K_cを超えると急激に同期が強まる(相転移が起きる)ことが知られています。

添付画像

Kuramoto model: K = 0.9K_c の場合

同期は起こらない。 pic.twitter.com/fiUa3ukDLI

タグ： Julia言語数楽

posted at 07:48:49

#Julia言語 #数楽

Kuramoto model: K = 1.0K_c の場合

同期が起こる起こらないの境目。 pic.twitter.com/FBlQjv07wr

タグ： Julia言語数楽

posted at 07:48:53

#Julia言語 #数楽

Kuramoto model: K = 1.1K_c の場合

K が K_c を超えると急激に同期が強まる。 pic.twitter.com/Nlwf5PLu7Z

タグ： Julia言語数楽

posted at 07:48:56

#Julia言語 #数楽

Kuramoto model: K = 1.2K_c の場合

K = 1.1K_c の場合よりも同期が強まっている。 pic.twitter.com/Ad8Kjq1SjV

タグ： Julia言語数楽

posted at 07:48:59

#Julia言語 #数楽

Kuramoto model: K = 1.3K_c の場合

「すべての2つの枡目の組み合わせ」で相互作用が起こっています。各人が残りの全員の状態に引っ張られている。

そのひっぱりの強さがある一定以上にならないと同期は起こらない。 pic.twitter.com/YBLxQpr825

タグ： Julia言語数楽

posted at 07:49:02

#Julia言語以上のような計算機実験がJuliaを使えばたったの10行のコードを書くだけで可能です。

ソースコードを見れば、どのような微分方程式を考えているかや、臨界値 K_c の値がどのように決まっているかもわかる。

ソースコード↓
nbviewer.jupyter.org/gist/genkuroki... pic.twitter.com/OFyb8GbcDM

タグ： Julia言語

posted at 07:52:11

#Julia言語ソースコード解説

1. パッケージの読み込み

2～3. 蔵本モデルの微分方程式の記述

dθ_i/dt = ω_i + K (1/N) Σ_j sin(θ_j - θ_i) (i=1,…,N)

θ_iはi番目の振動の角度による表現。
θ_iはmod 2πでのみ意味を持つ。
ω_iはデフォルトの角速度。iごとに違う。
Kは相互作用の強さを表す。 pic.twitter.com/GagqO4k1y9

タグ： Julia言語

posted at 08:22:57

#Julia言語

4. パラメータの設定

* m×nで表示
* d = ω_iのばらつき方を記述する平均0標準偏差2の正規分布
* v = ω_iの期待値

* K_c = 2/(π p(0)) (p(x)は左右対称な分布dの密度函数)。同期が始まる臨界値K_cはデフォルトの角速度ω_i達のばらつき方が大きいほど大きくなります。直観的には当然。 pic.twitter.com/mSxxvXLLpo

タグ： Julia言語

posted at 08:22:58

#Julia言語続き

* tmax = どの時刻まで計算するか
* a = 1.3 相互作用の強さ。後で相互作用の強さKをK=aK_cと定める。

5. モデルのパラメータ

θ₀ = θ_i達の初期値をランダムに決める
tspan = (0.0, tmax)
K = aK_c
ω = ω_i達を平均vばらつき方dでランダムに決める

続く pic.twitter.com/IR1qDWs7sw

タグ： Julia言語

posted at 08:22:59

#Julia言語続き

6. 微分方程式の数値解 sol を求める

7～10. sol からgif動画を作成。

JuliaのPlots.jlによるgif動画の作成はmatplotlibによるgif動画の作成よりもずっとシンプルで簡単です。

以前はmatplotlibでgif動画を作っていたのですが、Plots.jlに完全に引っ越してしまいました。 pic.twitter.com/LaBNrx0set

タグ： Julia言語

posted at 08:23:00

#Julia言語モデルのコード化には、微分方程式、パラメータ、初期値などを全部書く必要があります。その分だけの行数はどうしても必要。使用するパッケージの読み込みの行も必要です。これで6行消費。

残りの4行でgif動画作成。(最後のendを1つ前の行の行末に移動すれば全部で9行に減らせる) pic.twitter.com/us7YHHbYpd

タグ： Julia言語

posted at 08:25:41

チズチズ(Yuma Ochi) @chizu_potato

#Julia言語ほど、パッケージの読み込みとモデルの記述だけで微分方程式の数値解が求まってしまいます。視覚化の見栄えを良くするための工夫もシンプルに書けている。圧縮して書いているのにコードの可読性はそう悪くない。

こういう使い方をするにはJuliaは最強の道具だと言ってよいと私は思う。 pic.twitter.com/exYeSJgEEt

タグ： Julia言語

posted at 08:28:11

某教科書が手に入ったのでJuliaはじめるしかないか

タグ：

posted at 08:31:28

#Julia言語 DifferentialEquations.jlで求めた数値解 sol はこの場合には時刻 t のm×n行列値函数としての機能も持っていて、非常に便利です！

sol(t)はθ_i(t)達のm×n行列で、sin.(sol(t)) は sin(θ_i(t)) 達のm×n行列になります。sin.(sol(t))' はその転置になる。そのヒートマップを作画している。 pic.twitter.com/imIIph3Hz4

タグ： Julia言語

posted at 08:32:21

#Julia言語このたったの10行のコードの内容を1週間程度かけて理解すれば、確率分布、微分方程式、グラフの作画をJuliaで扱えるようになるはずです。

この10行分だけ理解すればよい。 pic.twitter.com/vYVYwDf7WX

タグ： Julia言語

posted at 08:34:00

ロボ太 @kaityo256

Masa Yamamoto予測誤差が大き @mshero_y

@genkuroki おお、ありがとうございます。f(E[X])とE[f(X)]がずれるのはテイラー展開すれば式としては出てきますが、「接線に関する期待値」だと思うと、ずれる方向と、ずれの大きさが二次の微係数に依存することが直観的にわかりやすいですね。

タグ：

posted at 08:46:24

ダイナマイト十五浪 @dynamite15RONIN

いやー、この10行は本当にためになる。
@genkuroki 先生に感謝!!

タグ：

posted at 09:32:04

@genkuroki 1.5.3環境でエラーでたんですが、
1.6前提だったりしますかね pic.twitter.com/AZ73AHiUf0

タグ：

posted at 09:45:53

実行列 A の転置は
{}^t A でいいんじゃないか？ pic.twitter.com/0ajSPFIQJy

タグ：

posted at 10:21:19

github.com/JuliaLang/juli...

タグ：

posted at 10:21:20

github.com/JuliaLang/juli...

タグ：

posted at 10:21:20

A'ᵀ (A'\^T <TAB>)が transpose として使える予定だがこれは A' adjoint して tranpose してるように見えるので misleading では？という議論

タグ：

posted at 10:21:20

@dynamite15RONIN ごめんなさい！私はnightly buildを使っています！

DifferentialEquations.jl を使う場合にはv1.6以上が推奨！

タグ：

posted at 10:24:07

2x を 2 * x として看做されるロジックってどのレベルで処理されてるんだ？（実装どこ？）

#Julia言語

タグ： Julia言語

posted at 10:24:46

#Julia言語私は数日前のnightly buildを使っています。

DifferentialEquations.jlを使う場合には「Julia v1.6以上推奨」ということにしておいた方が多分よいです。最初の読み込みにかかる時間がv1.5だと無駄に長くなってしまいます。

タグ： Julia言語

posted at 10:25:28

(｢・ω・)｢ｶﾞｵｰ @bicycle1885

#Julia言語 Plutoノートブックも用意しました。添付画像のようなことをできます。

gist.github.com/genkuroki/a50f...

以下のリンク先と同様の方法で上のリンク先のURLをPlutoで貼り付ければ使えます。ただし、

pkg> add DifferentialEquations

も忘れずに。

twitter.com/genkuroki/stat... pic.twitter.com/21GnjYebsK

タグ： Julia言語

posted at 10:27:53

@MathSorcerer このへんgithub.com/JuliaLang/juli...

タグ：

posted at 10:28:39

#Julia言語蔵本モデルについて、こういう動画も作りました。

初期条件は一様分布なのですが、すみやかに山の形にまとまって同期するようになります。 pic.twitter.com/K0t1nnEpMc

タグ： Julia言語

posted at 10:30:12

山かつ @tdkmam2

魚のフライを朝食に出したら娘が金魚の数が減ってないか数えてたww確かにww pic.twitter.com/qJ1kvbl0pC

タグ：

posted at 10:51:39

@dynamite15RONIN #Julia言語確認してみました。

蔵本モデルの部分のコードは v1.5.4 でも動きました。
↓
nbviewer.jupyter.org/gist/genkuroki...

パッケージのインストールに問題があるのだと思います。
pkg> update が必要なのかもしれません。

タグ： Julia言語

posted at 11:15:20

RochejacMonmo @RochejacMonmo

ずっと疑問なんだけど、新学習指導要領のような学習のグランドデザインに影響を与えている人たちはどういう人たちなの？視学官という立場の人はどういう役割を果たしているんだろう？端的に言って新学習指導要領の実質的な作成責任者は誰になるんだろう？誰がこれについての説明責任を負っているのか？

タグ：

posted at 11:32:49

こいなぎ @naginyan135

【級位者向け実戦型詰将棋part482(松田茂行先生作)】
これを詰ますことができた者だけがこれを詰ますことができる。 pic.twitter.com/M6mzcdcRuj

タグ：

posted at 12:01:26

@kaityo256 そうなんです！

接線を1本図示するだけで、バイアスが生じる理由とバイアスの向きと大きさについて(数式に頼らない)「一目瞭然」的な理解が可能になるんです！

タグ：

posted at 12:30:05

「函数の凸な部分に接線を引くとどう見えるか」は余りにも当たり前の話なのですが非常に重要。

そういう意味でJensenの不等式の証明の中身は非常に大事。

微積分を教える仕事が割り振られた場合には必ずJensenの不等式の話もしている。

これ、高校でも教えた方がよいと思う。 #数楽

タグ：数楽

posted at 12:33:57

#Julia言語 #数楽

相互作用の強さが臨界値の2倍の場合。めっちゃくちゃ同期しまくっている！

上で紹介したPlutoノートブックで作れます。 pic.twitter.com/iazcHsUzpd

タグ： Julia言語数楽

posted at 12:50:38

#Julia言語 #数楽

1つ前のツイートの場合(K = 2K_c)におけるθ_i達の分布の動画。

初期条件は一様分布。

各θ_iごとに相互作用無しのときのデフォルトの周期は違う。異なる周期を持つ振動子であっても、蔵本モデルではこのように同期してしまう。 pic.twitter.com/sXuezPv8kP

タグ： Julia言語数楽

posted at 12:53:34

#Julia言語

DifferentialEquations.jl はものすごく便利。例えば数値解が「函数」の形式で得られる！(こういうインターフェースが定義されているのは本当にありがたい)

しかし、Julia v1.5以下だとusingにかかる時間が長い。Julia v1.6以上で使うことがお勧め。

nightly buildでも使えています。

タグ： Julia言語

posted at 12:57:12

#Julia言語添付画像のように、v1.5.4と数日前のnightly build (v1.6以上でもほぼ同じはず)では、最初のusingにかかる時間が全然違う。

一度、v1.6以上の世界に慣れると、もうv1.5には戻れなくなります(笑)

Juliaを使い続けると大体数ヶ月ごとに「前よりも使い易くなった」と感じることができます。 pic.twitter.com/80LyHf7ghk

タグ： Julia言語

posted at 13:23:21

#Julia言語継続的な改善を「学習」してしまうとどうなってしまうか？

①試しにnightly buildも使ってみようと思うようになる。
②nightly buildはひどく壊れていることがある。
③そのとき、「学習」の効果によって、「大きな改善が約束されていることを意味する」と感じるようになる(笑)

タグ： Julia言語

posted at 13:27:16

#Julia言語現在では(相対的に)nightly buildもかなり安定しているし、壊れているnightly buildにぶちあたっても、壊れていない段階のnightly buildに戻せば使い続けられます。

タグ： Julia言語

posted at 13:36:06

#Julia言語はバイナリもまとめて面倒をみてくれるパッケージマネージャーが優秀なので、実験的に新しいバージョンを入れてみることへの心理的障壁が低いです。

自分専用のパッケージ集の大規模破壊の心配がほぼない。

Pythonでは何度もやらかしたことがある。

タグ： Julia言語

posted at 13:39:48

#Julia言語以下のリンク先のP値を扱うコードは書き直した。現在のバージョン

nbviewer.jupyter.org/gist/genkuroki...

ならv1.5.4でも動きます。

nightly buildでは

range(a, b; length=n)

の代わりに

range(a, b, n)

と書けるようになっています。それを上の形式に戻した。

twitter.com/genkuroki/stat... pic.twitter.com/GiipZklbY4

タグ： Julia言語

posted at 13:45:05

#Julia言語 ⪅(x, y) = x < y || x ≈ y は離散分布を浮動小数点数で扱うときにはほぼ必須の函数です。

理論的には x ≤ y という比較で十分であっても、浮動小数点数 x, y の計算では、x > y となっていても、"x ≤ y" とみなさなければいけない場合が出て来ます。

⪅ は x ⪅ y の形式で使えます。

タグ： Julia言語

posted at 13:49:57

#Julia言語

pval(d, k) = sum(pdf(d, j) for j in support(d) if pdf(d, j) ⪅ pdf(d, k))

は分布dとデータkについて「分布d内でデータk以上に生じ難いjのどれかが分布d内で生じる確率」です。

生じ難さで「偏り」を測るときの「モデル内でデータ以上の偏りが生じる確率」＝P値の定義そのもの。

タグ： Julia言語

posted at 13:53:20

#Julia言語「定義に戻って数学的にシンプルに考える」をできている人にとってJuliaは天国で、定義に戻ってシンプルに考えた式をそのままJulia語に直せば計算したいものが計算できてしまいます。

P値はブラックボックス扱いするべき数値ではなく、各場合ごとに自分で定義を考えるべき類のものです。

タグ： Julia言語

posted at 13:55:55

#Julia言語 d = Binomial(n, p) のとき、データkに関するpの信頼区間はP値がα以上になるpの集合のことです(これが定義)。データkが分布dで生成されているとき、pがその信頼区間に含まれる確率は

prob_ci_contains_p(d, α=0.05) = sum(pdf(d, k) for k in support(d) if pval(d, k) ≥ α)

タグ： Julia言語

posted at 14:00:18

#Julia言語 P値やモデルのパラメータ値が信頼区間に含まれる確率は1行で定義された函数で計算できる！

しかも、そうした方が可読性が高くなる！

それらの函数は、英単語の意味を知っていれば、Juliaを知らなくても何を計算しているかがわかるように書ける。

これが抽象化の威力です。 pic.twitter.com/71WYzP1jcJ

タグ： Julia言語

posted at 14:07:27

#Julia言語「二項分布モデルでモデルのパラメータの値が95%信頼区間に含まれる確率を計算してプロットしなさい」という練習問題を解いておくことは、信頼区間ユーザーになりたい人にとって必須だと思います。

JuliaならばP値函数の実装も自分で行ってもそれの問題を10行で解けてしまうわけです。 pic.twitter.com/9iciSOGAu8

タグ： Julia言語

posted at 14:10:11

#Julia言語 JuliaのDistributions.jlでは「確率分布」をJuliaの変数dに格納できます。確率分布をdの1文字で表現し、その確率密度函数もpdf(d, x)と書ける。

Distributions.jlでは「確率分布」の概念がきちんと抽象化されている。そういうことができているならJulia以外でも同様のことをできます。

タグ： Julia言語

posted at 14:12:28

#Julia言語添付画像中では二項分布での信頼区間を計算する函数が2行で書けています。通常の書き方をすると、

function ci(n, k, α)
CI = find_zeros(p -> pval(Binomial(n, p), k) - α, 0, 1);
k == 0 ? (0.0, CI[end]) : k == n ? (CI[1], 1.0) : (CI[1], CI[end]))
end

くそシンプル！ pic.twitter.com/yN5Xf05Lmg

タグ： Julia言語

posted at 14:18:39

#Julia言語 find_zeros(f, a, b) は区間[a, b]内での函数fの零点の全体を配列で返してくれる函数です。

函数 f(p) = pval(Binomial(n, p), k) - α の零点は二項分布モデルのP値がαになるパラメーターpの値のことで、それらを求めることは信頼区間の計算そのものになっています。

タグ： Julia言語

posted at 14:20:44

ダンボルギーニ斎藤ጿኈ ቼ ዽ ጿ @ritzberry

#Julia言語後で数値積分ライブラリを使うことになるとしても、簡単な数値積分函数を自分で書いてみるという経験は大事。

オイラー法さえ自分で実装したことがない人が、微分方程式のソルバのライブラリを使うのは危険だと思う。

自分でP値や信頼区間を計算する函数を書く経験もあった方がよい。

タグ： Julia言語

posted at 14:25:07

以下の結果を見ればわかるはず。julia はとっても天文学者向け。

julia> pi = 1
1
julia> pi
1

タグ：

posted at 14:36:06

ザード＠ @world_fantasia

Juliaはとりあえず使えそうだけどRustは本腰入れてやらんと使えるようにはならんなこれ

タグ：

posted at 17:02:39

TaKu @takusansu

参考情報
昔の中学数学教科書の倍数の扱い
8254.teacup.com/kakezannojunjo...

twitter.com/temmusu_n/stat...

タグ：

posted at 17:20:57

#Julia言語上の方で二項分布モデルのP値と信頼区間の1～2行による実装法を解説したが、2×2の分割表の独立性に関するFisher検定のP値も信頼区間も1～2行で書ける。

しかもそうやって実装した結果はRのfisher.testよりも良い性質を持っていたりする。

ソースコード↓
nbviewer.jupyter.org/gist/genkuroki... pic.twitter.com/W3vaHzY2Vm

タグ： Julia言語

posted at 17:45:37

マナマの生マナマコ @chor0sK

はじめてJuliaのマクロ書いた

タグ：

posted at 17:47:20

#Julia言語

Julia集合の動画も10行で作れる。

余裕のプログレスメーター付き(笑)

どこまで進んだかを表示させたい人には参考になるはず。

(Mandelbrot集合の動画も同様の方法で作れるはず)

ソースコード↓
nbviewer.jupyter.org/gist/genkuroki... pic.twitter.com/BnRovywF2A

タグ： Julia言語

posted at 17:48:34

#Julia言語でJulia集合の動画を作成

ソースコード↓
nbviewer.jupyter.org/gist/genkuroki...

この手の作品では色の付け方が結構重要なポイントになることが多い。これはカラーマップとして:gist_earthを使っている。

この手のことも全部10行で可能。この場合には余裕でプログレスメーターも設置できた。 pic.twitter.com/GZIbHMupEw

タグ： Julia言語

posted at 17:52:23

#Julia言語 Juliaの型について十分な理解がない段階でJuliaで型を明示的に書くと、大抵の場合ろくなことにならないし(バグの原因になる)、理解が進むと、型を明示的に書いた方が良いという考え方自体が技術的に劣っている考え方だと気付きます。

Juliaでは型を明示せずに、型の伝搬で考える。続く twitter.com/mrsekut/status...

タグ： Julia言語

posted at 19:19:05

#Julia言語私自身がやらかした失敗の例

① function f(x::Vector{Float64}) ～ end

のように引数の型を明示した函数を定義し、その函数を使ったプログラムが正常に動作していた。

② @ viewマクロを使った最適化を行った。

③その途端に正常に動いていたプログラムが動かなくなった！😭

続く

タグ： Julia言語

posted at 19:19:06

#Julia言語その原因は

function f(x::Vector{Float64}) ～ end

と函数の引数の型を Vector{Float64} に明示的に宣言してしまっていたことが原因です。その「@ viewによる最適化で動かなくなった」という問題は

function f(x) ～ end

に書き直せば解決しました。続く

タグ： Julia言語

posted at 19:19:07

#Julia言語数値計算ではなく、文字列処理を多数やっている人なら、私と同様の失敗を

function f(x::String) ～ end

と書いてやらかしていたりすると思います。

SubStringはStringではないので、これだと思わぬ所でプログラムが動かなくなりがち。

@ viewで作ったSubArrayはVectorではない。続く

タグ： Julia言語

posted at 19:22:18

#Julia言語上のような失敗は

function f(x::AbstractVector{Float64}) ～ end

や

function f(x::AbstractString) ～ end

と書いていれば防げました。

しかし、

function f(x::AbstractVector{Float64}) ～ end

には別の致命的な欠点があります。続く

タグ： Julia言語

posted at 19:24:36

ハードオフで550円で買ったやつなんですけど、多分元の持ち主が鉄道関係者。

あと牌の背が竹なんですが、牌も象牙の可能性がある。 pic.twitter.com/wWDBHJKBmg

タグ：

posted at 19:26:51

#Julia言語は composability で優れています。

具体的には、例えば、Juliaで適切に書かれた微分方程式のソルバを使っていれば、後でパラメータの値に幅を持たせたときの微分方程式の解の挙動の視覚化を新たなコードを追加せずに実行できます。

以下のリンク先スレッドに実例があります。続く twitter.com/genkuroki/stat...

タグ： Julia言語

posted at 19:29:51

「長鐡ルール」とかいう謎ルール。 pic.twitter.com/mWVR2awXXg

タグ：

posted at 19:32:16

#Julia言語新たなコードを追加せずに、パラメータの値に幅を持たせた場合を扱うには、「幅を持つ数値」の型を定義し、微分方程式のソルバにそういう型の数値を使った場合の微分方程式を解かせればよい。 twitter.com/genkuroki/stat...

タグ： Julia言語

posted at 19:35:36

#Julia言語だから、

function f(x::Vector{Float64}) ～ end

のように書いた途端に、Float64型専用の「幅を持つ数値」の型では使えない函数になってしまい、Juliaの強みであるcomposabilityを活かせなくなってしまいます。続く

タグ： Julia言語

posted at 19:35:37

twitter.com/pheebin/status...

タグ：

posted at 19:37:14

#Julia言語 Float64型や「幅を持つ数値」の型の多くがReal型のsubtypeであると知った人が

function f(x::Vector{Real}) ～ end

と書くと、ほとんど全く使えない函数が出来上がります。なぜならば、Vector{Float64}型はVector{Real}型のsubtypeにならないからです。続く

タグ： Julia言語

posted at 19:40:49

#Julia言語

function f(x::Vector{Real}) ～ end

ではなく

function f(x::Vector{<:Real}) ～ end

と書かなければいけないことを知っておく必要がある。

以上の解説をよんで「うわ！こんな面倒ならJuliaを使えない！」と思った人は私の仲間です！(笑)

シンプルな解決策があります！続く

タグ： Julia言語

posted at 19:40:51

twitter.com/pheebin/status...

タグ：

posted at 19:41:24

#Julia言語

シンプルな解決策：函数の引数の型の指定は必要最小限にする。基本的に函数の引数の型の指定をしないことにする。

無駄な記述が減ってコードもすっきり見易くなります(笑)
↑
これは冗談ではないです。

函数の引数の型の指定の有無はJuliaでは計算効率に何も影響しません。続く

タグ： Julia言語

posted at 19:44:07

#Julia言語たたし struct の定義で

struct Foo
a
b
end

と書くのはダメです。計算速度が露骨に落ちます。しかし、

struct Foo
a::String
b::Float64
end

と書くと、上で説明したのと似た問題が起こる場合がある。

struct Foo{A, B}
a::A
b::B
end

がお勧め。

タグ： Julia言語

posted at 19:47:03

鉄のひと的には面白そうなやつ。 pic.twitter.com/wKlnGlKOVK

タグ：

posted at 19:49:12

#Julia言語要するに、具体的な型名をほとんど書かずに、Juliaの便利な機能(speed! composability! ...)だけを美味しく利用することができるわけです。

しかし、コードを書くときに支払うべき新たな税金はあります。

それはtype stabilityの確保。

型の伝搬の安定性と言う方が分かり易いかも。

タグ： Julia言語

posted at 19:49:45

みゆき @miyuki_MathT

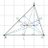
今年度も超算数の【0は何の倍数でもない】の被害者が出ました
もうこれ確認するの手間だから、小学校で習ってしまったであろう嘘をまとめて、忘れるように指示する資料作った方が良いな

「4の倍数の集合X」
を複数パターン書いてください

偶数を羅列したベン図がありましたが、0が避けられましたw

タグ：

posted at 19:58:26

#Julia言語は、JITコンパイラなので、函数の実行時に完全にわかっている引数の具体的な型に合わせて最適化されたネイティブコードにコンパイルすることを試みます。

タグ： Julia言語

posted at 19:58:37

#Julia言語例えば f(x)=x^2 をf(123)と実行するとxがInt64型専用のネイティブコードを、f(12.3)ならFloat64型専用のネイティブコードを、f("abc")ならString型専用のネイティブコードにコンパイルしてから実行します。(f("abc")は"abcabc"になる)

タグ： Julia言語

posted at 19:58:39

#Julia言語適切にコードを書けば、引数の具体的な型から函数の値の具体的な型が一意的に決まります。これが型安定の最も易しい場合です。

f(x)=x^2よりも複雑で局所変数を持つ函数では、局所変数の具体的な型が引数の型から一意的に決まるように(型安定になるように)書くことが、Juliaの流儀です。

タグ： Julia言語

posted at 19:58:41

みゆき @miyuki_MathT

天むす名古屋 Temmus @temmusu_n

笑い事じゃないけどね
まあ、訂正はすぐに済むけど(だから良いという話でもない)

タグ：

posted at 19:59:22

@takusansu #超算数 1978年版の中学校数学教科書、ありがとうございます。啓林が0を倍数と定義していると。当時は現代化の次の指導要領が1977年に告示され、81年からの施行を準備している時代ですね。啓林については現代化の教科書を準備中に塩野直道が死去したことの影響など、調べることがでてきました。

タグ：超算数

posted at 19:59:47

#Julia言語要するに

function f(x)
～
end

のように引数の型をしてせずに函数を書くときには、xの具体的な型が想定内の何であっての、その具体的な型が函数内の他の変数の具体的な型を適切かつ一意的に決まるように書くことを目指します。

型の明示ではなく、型の伝搬で勝負するわけです。続く

タグ： Julia言語

posted at 20:02:07

点数計算の一部なんですが、「ヤス上りとガメクリのうた」とは🤔 pic.twitter.com/7yNfy5bq0w

タグ：

posted at 20:03:14

#Julia言語型の伝搬の仕方を人間の頭の中でシミュレートし切るのは無理です。型の伝搬の様子を表示してくれる便利なコマンド(マクロ)があります。

f(x) = x^2

@ code_warntype f(2)

@ code_warntype f(2.0)

@ code_warntype f("a")

を実行してみると良いと思います。@ 直後の空白は削除。

タグ： Julia言語

posted at 20:05:49

#Julia言語 @ code_warntype は型の伝搬の安定性が崩れている場合には強い警告色でその部分を表示してくれます。

ごちゃごちゃっと意味不明の複雑な表示を細かく見ずに、強い警告色で表示された部分がもとのコードのどの部分に対応するかのみに意識を集中すれば、初心者であっても実用になります。

タグ： Julia言語

posted at 20:09:53

#Julia言語例えば

exp_approx(x, n=10^6) = (one(x) + x/n)^n

というコードは近似的にexp(x)を計算してくれる函数です。

one(x)は多くの場合にxと同じ型の1になる。このように書いておくと、正方行列xにも適用可能になる(添付画像1)。

添付画像2は@ code_warntypeの例。 pic.twitter.com/GwsAedBY1l

タグ： Julia言語

posted at 20:33:04

#Julia言語微分方程式のソルバは本質的に上の exp_approx(x, n) の一般化とみなせます。

Juliaで適切に微分方程式のソルバを書けば、exp_approx(x, n)のように、Float64, Float32, BigFloat, ComplexF64, Matrix{Float64}, etc.と多数の型の入力に対応しているものを作れます。

タグ： Julia言語

posted at 20:36:36

#Julia言語そして、そのソルバは実行時に入力の具体的な型に合わせて最適化されたネイティブコードにコンパイルされてから実行されることになります。

入力が「幅を持つ数値」なら「幅を持つ数値」の型専用のネイティブコードにコンパイルされてから実行されます。

タグ： Julia言語

posted at 20:38:58

#Julia言語これは同じようなコードを繰り返し書く手間を大幅に減らしてくれます！

そして、それを支える基本的な考え方は、型の明示で頑張ろうとせずに、型の伝搬を適切に記述するという考え方です。

上の例では one(x) のような書き方が型の適切な伝搬を支えています。

タグ： Julia言語

posted at 20:44:33

#Julia言語では、「Float64型を与えて、Float64型の値を返す函数を書く」という発想をせずに、

* 引数の具体的な型に合わせて、適切な型の値を返す函数を書く。

* 函数の引数の具体的な型から函数内の局所変数の型が自動的に決まるように書く。

のように考えます。

タグ： Julia言語

posted at 20:50:38

Yasu @yasu_eng_code

Julia 勉強中だけどほんとに Python を超えられるか楽しみ半分、勉強の楽しさ半分ってとこかな。

Juliaで常微分方程式を解く qiita.com/P_Fermat/items... #Qiita @erin_yagokoroより

タグ： Qiita

posted at 21:20:03

残り14件のツイートを見る

TaKu @takusansu

天むす名古屋 Temmus @temmusu_n

@temmusu_n しかし【倍数・約数については，0は除いて考えることにする】とあるのが気になります。

タグ：

posted at 21:20:44

@takusansu なんでこう残念な一文を付け加えるんでしょうかね。検定が理由じゃないかと思いますけど。

タグ：

posted at 21:24:35

OokuboTact　大久保中二病中年 @OokuboTact

#Julia言語 NASAでJuliaがどのように使われているかについては以下のリンク先のスレッドを参照。 twitter.com/genkuroki/stat...

タグ： Julia言語

posted at 21:33:25

@temmusu_n @takusansu ＞　新数学1 大日本図書K．K．昭和53年
＞　“ここでは，倍数は自然数の集合で考えているので，0は取り除かれる”

これは小学校の考えそのままですね

twitter.com/OokuboTact/sta...

タグ：

posted at 21:45:03

天むす名古屋 Temmus @temmusu_n

#Julia言語【ネタ】

添付画像①

pi = 1 としてしまうと「しまった！」となるのですが、Base.pi に元の pi は残っています。sum = 0 としても、Base.sum は使える。

添付画像②

Base.:+(x::Int, y::Int) = nothing

😱😱😱😱😱 twitter.com/ritzberry/stat... pic.twitter.com/3xBFN09wv5

タグ： Julia言語

posted at 21:51:13

@OokuboTact @takusansu そういえば！　倍数、約数が、分数計算の補助概念であった時代との整合性が現在でも保たれていることはすごいですね！#超算数

タグ：超算数

posted at 22:11:53

太田伸二 @shin2_ota

ぬまち　#疑わしきはバツせず @numachi11111

仙台地裁はかなりWEB会議が浸透して、弁準で出かけることがほとんど無くなりました。
行くのは大きな事件の弁論か、和解成立の弁準くらい。だいぶ楽です。 twitter.com/ssk_ryo/status...

タグ：

posted at 22:17:33

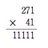
たかが足し算を分類しまくって、十を聞いて一を知る。
かけ算の順序を区別して、十を聞いて一を知る。
割り算を分類して、十を聞いて一を知る。
長方形の集合から正方形を取り除いて、十を聞いて一を知る。
割合なんて、ただの○倍ってだけなのに、3 用法などと区別し、十を聞いて一を知る。
やばい。 twitter.com/tsatie/status/...

タグ：

posted at 22:44:24

Hiroo Yamagata @hiyori13

@mk_sekibang cruel.hatenablog.com/entry/20121118...

タグ：

posted at 23:17:46

あんちもん2 @antimon2

@abap34 `Variable` を定義時に `struct Variable <: Number ～ end` とか `struct Variable <: Real` とかしたら、他の `Number` との promote は定義済だから `Base.:+(x1::Variable, x2::Variable)`（と`promote_rule`と`convert()`）だけ定義すれば他の数値との四則演算はできると思うですがいかが？

タグ：

posted at 23:20:35

#Julia言語固定されたX,Yについて

f : X → Y

を定義するという考え方ではなくて、

f : (?) → Φ(?)

を定義するという発想。

?として具体的な型を与えると、fの終域 Φ(?) が具体的な型として決まるように書きたい。(fの定義中で間接的にΦを記述する。)

fの型は「fそのもの」になる。

タグ： Julia言語

posted at 23:46:32

あんちもん2 @antimon2

@abap34 思いついたまま殴り書いたので少し説明おかしかった。`Base.:+(x::Number,y::Number)=+(promote(x,y)...)` が定義済だから`Variable`を`Number`のsubtypeにすれば`Variable`どうしの足し算とpromoteruleとconvertだけ定義すればOK、が正しいです。

タグ：

posted at 23:47:28

#Julia言語信頼区間函数をもっとまともなものにした。

二項分布モデルの場合

function ci(n, k, α)
CI = find_zeros(p -> pval(Binomial(n, p), k) - α, 0, 1)
isone(length(CI)) ?
CI[1] < 0.5 ? (0.0, CI[1]) : (CI[1], 1.0) : (CI[1], CI[end]))
end

nbviewer.jupyter.org/gist/genkuroki... pic.twitter.com/f4ta44vhga

タグ： Julia言語

posted at 23:53:53

あんちもん2 @antimon2