黒木玄 Gen Kuroki(@genkuroki)/2021年09月24日

@genkuroki そして行ったことなしに言及したことは反省するつもりはないと開き直ってます
note.com/sawawww/n/ndc8...

どうも「主語がまだ小さい」とか言われるような身内スペースしてたらしいのでエコーチェンバーして先鋭化してそうですね

タグ：

posted at 03:11:34

Jacob Quinn @quinn_jacobd

Joined the #JuliaLang twitter community today. Let's see where this goes. Always interested in more focused avenues for content I'm interested in: twitter.com/i/communities/...

タグ： JuliaLang

posted at 03:52:49

こばしり @cobaetal

物理学会怖いって思われてるみたいだけど、

超偉い理論物理の大家の指摘を、学生が「先生は〇〇な勘違いをしているので、私の結論は物理的に正しい」とバッサリと切り捨てる場面も見た事ある

物理学の前では上も下もなくフラットという雰囲気なのは知られて欲しいな

色々是正すべき所はあるけどね

タグ：

posted at 06:46:32

癒される動物 @cutest_animal1

こんな風に甘えられたい✨ pic.twitter.com/v6xU1UWQab

タグ：

posted at 08:13:02

浅水屋剛（Takeshi Asamiz @asamizuya

#超算数上の方で【中島健三以前に回帰】だと嘆いてみせたのは煽りすぎですね。おそらく、割合に関する有害な指導は途切れることなく続いてきたというのが実態なんでしょう。60-79年ごろについても調べれば何か出てくる見込みが高い。80年代からはくもわ、はじきが観察されます。

タグ：超算数

posted at 09:39:43

うわ…。 twitter.com/genkuroki/stat...

タグ：

posted at 10:31:31

OokuboTact　大久保中二病中年 @OokuboTact

Neyman-Pearsonの補題は帰無仮説と対立仮説の確率分布q(x),p(x)がデータと無関係に決まっている場合の尤度比検定に関する結果。

一方、単に尤度比検定と言う場合には、尤度比を取る確率分布をデータを使った最尤法で決定する場合を含みます。その場合はNeyman-Pearsonの補題と異なる話になります。 twitter.com/student_stats/...

タグ：

posted at 10:34:02

OokuboTact　大久保中二病中年 @OokuboTact

#超算数

チョー算数がネットで話題になる流れ

トンデモ採点がネットにアップされる
　　　↓
数学の常識ある人が「この採点はおかしい」と指摘する
　　　↓
ネットで話題になる

タグ：超算数

posted at 11:26:47

（補足）　　#超算数

ほとんどの人は小学校でどんな算数教育が行われているのか知らないわけです。
だからトンデモ採点を見て驚くわけです

タグ：超算数

posted at 11:29:01

#統計帰無仮説と対立仮説の確率分布q(x),p(x)がデータと無関係に決まっている場合の尤度比検定に関するNeyman-Pearsonの補題の証明は非常に易しいです。

一方、最尤法を使う対数尤度比のχ²検定の基礎付けはWilks' theoremの話になり、証明はNPの補題よりもずっと難しくなります。

タグ：統計

posted at 11:41:39

steinberg @rackowsteinberg

@cobaetal @genkuroki 普段の授業からして日常的にそうだしね

タグ：

posted at 11:44:44

#統計 Wilks' theoremは以下の場合にも使われるので、非常に基本的なので知らないとかなり苦しくなる。

* 分割表の独立性のχ²検定の基礎付け
* 例えば2×2の場合の独立性検定での自由度は1
* より一般に「自由度」の概念の正確な把握
* 仮説検定とAICによるモデル選択の比較

タグ：統計

posted at 11:45:36

#統計中心極限定理のコンピュータを使った数値的確認(易しい)をやってみたことがある人は、Wilks' theoremについてもコンピュータで数値的確認をやってみた方がよい(こちらも易しい)。

gist.github.com/genkuroki/6667... twitter.com/genkuroki/stat... pic.twitter.com/FLJOhZsfUm

タグ：統計

posted at 11:51:45

the hash @yosuke_hash

式みてもわけわからんが数値計算の結果を（グラフで）見ればなんとかなる、というのは人間の大いなる知恵だなあと思う。MCMCとかもそうだと理解している。 twitter.com/genkuroki/stat...

タグ：

posted at 11:55:24

患者さんの自由研究が、予想をはるかに突き抜けた完成度です😊🎉
50ページ近くあります。あとがきにある医療リテラシーの高さは、小学生とは思えないレベル…なお、参考文献リストまであるという徹底ぶり(°Д°)
感動したので、(許可をいただき)一部を共有します。1/n pic.twitter.com/rZhK3uUngy

タグ：

posted at 13:07:08

病態のつかみ方がプロ。
そして、イラストがすごく分かりやすいでづ😊
アトピービジネスまで踏み込むとは…やるなあ…😌
2/n pic.twitter.com/cxiUOXeu7m

タグ：

posted at 13:12:00

アトピー性皮膚炎の治療を、的確につかんでるなあ…😊 pic.twitter.com/E9HhrR7jkc

タグ：

posted at 13:14:37

舌下免疫療法の説明もうまい。
樹状細胞の解説まである…(°Д°)
4/n pic.twitter.com/xj3mFpXOZK

タグ：

posted at 13:17:07

最高にすごいのがあとがき。
ここまでの医療リテラシーは、大人でもなかなか持てないんじゃないだろうか…🤔
5/5 pic.twitter.com/sG9kzEuoPT

タグ：

posted at 13:18:53

Hiromitsu Takagi @HiromitsuTakagi

個人番号（マイナンバー）をハッシュ変換した符号も、法律上、個人番号（マイナンバー）であることを…

タグ：

posted at 13:39:21

「名乗る」云々はまさに表面的な話。

そのYuta SAWAさんは

【主語を大きくしたのは炎上狙いだからですね】
物理学会に行ったことは【無いです。】

と言っている。😱

炎上するならYuta SAWAさん個人の態度が主に非難される形で炎上して欲しい。

学会をよりよくするための議論と分離するべき。 twitter.com/kikumaco/statu... pic.twitter.com/OUlGp0Rh14

タグ：

posted at 13:44:09

mattn @mattn_jp

なんやの、このかた pic.twitter.com/MMZLLAAVLs

タグ：

posted at 13:54:54

【ねこ[アレルギー]のめんえきりょうほうの研究も進んでいるらしい　ワーイ！】

ねこ好きらしい。くそかわいい。 twitter.com/ped_allergy/st...

タグ：

posted at 13:55:50

もるてん @iitenki_moruten

今日はこれから友達の家に泊まりに行ってJuliaしてきます pic.twitter.com/xsKVH4QP59

タグ：

posted at 15:52:06

西村賢 @knsmr

IPO後に時価総額1兆円に届くかもとも言われてるGitLabは、2011年にウクライナのエンジニアが、水道も来ていないような家で1人で始めたプロジェクト。すごい。

（画面はS-1資料にあるGitLab CEOの巻頭辞） pic.twitter.com/mnJGiFRAGG

タグ：

posted at 16:08:44

#Julia言語離散分布の場合には、ヒストグラムではなく、累積分布函数をプロットした方が安全です。

ただし、添付画像は累積分布函数cdfではなく、その補集合版のccdefです。

Wilks' theoremが予言する自由度のχ²分布でよく近似できていることが分かる。

gist.github.com/genkuroki/6667... pic.twitter.com/O70izYNKiR

タグ： Julia言語

posted at 17:12:37

#統計各帯(ビン)の幅の設定によってヒストグラムの印象は大幅に変わる場合があるので要注意。

そういう恐れがある場合には、累積分布函数や経験累積分布函数をプロットするとよい。

累積分布函数間のL¹距離はp=1のWasserstein距離に一致する。

タグ：統計

posted at 17:15:37

#統計 kernel density estimation で「ならした」結果をプロットする場合にも、ヒストグラムと同様の注意が必要。KDE適用時のパラメータによって印象が大きく変わる。

「累積分布函数cdfや経験累積分布函数ecdfをプロットする」というアイデアも身につけておいた方がよい。

タグ：統計

posted at 17:18:23

#統計 Wilks' theoremの内容は本質的に

n次元のW₁内を動くパラメータwを持つ確率分布p₁(x|w)とそれをW₁のn-d次元部分空間W₀に制限して得られるp₀(x|w)=p₁(x|w) for w∈W₀の2つで対立仮説H₁と帰無仮説H₀をモデル化したときの、χ²検定で使うχ²分布の自由度はdでなければいけないこと

です。

タグ：統計

posted at 17:55:19

#統計要するに、パラメータを制限する前のモデルとパラメータの自由度をd減らして得られるモデルをデータの尤度を使って比較するときの自由度がdになるということです。

パラメータ空間の次元が何次元下がったかが、χ²検定の文脈における自由度になります。

これは非常にクリアな説明です。

タグ：統計

posted at 17:57:54

#統計すでに定式化されて証明されているかもしれませんが、特異モデルが絡むケースでのベイズ版のWilks' theoremは誰かが定式化して証明するべき基本的な事柄の1つだと思います。

タグ：統計

posted at 18:00:59

#統計仮説検定は、対立仮説と帰無仮説が「パラメータ空間を制限する前のモデル」と「次元が相対的に小さな部分空間にパラメータ空間を制限して得られるモデル」のモデル選択の一種になっている場合が非常に多いです。

その場合には仮説検定とAICによるモデル選択を直接比較できます。

タグ：統計

posted at 18:04:52

Mark Kittisopikul ht @markkitti

@loicaroyer #Python and #JuliaLang work quite well together. pic.twitter.com/q8XUaAmjkD

タグ： JuliaLang Python

posted at 18:06:05

#統計通常のAICによるモデル選択がすべてのモデルを平等に扱うのですが、上記のケースにおける対数尤度比のχ²検定は帰無仮説側のモデルを「えこひいき」するAICによるモデル選択と数学的に一致します。

そして、AICは上記のケース以外の任意のモデルの比較でも使える強みを持つ。

タグ：統計

posted at 18:09:20

#統計中学校数学での箱ひげ図の利用について「これはやめて欲しい」と思うような内容の解説を発見しました。

rimse.or.jp/report/pdf/Rim... のpp.2-6
藤井良宜、中学校数学におけるこれからの統計教育、2018

予備知識：以下のリンク先での箱ひげ図の適切な使用先に注目(添付画像の赤線で囲まれた部分) twitter.com/t_weissgerber/... pic.twitter.com/BVCbd0rbMT

タグ：統計

posted at 18:22:21

#統計添付画像はどれも

藤井良宜 (2018)
rimse.or.jp/report/pdf/Rim... pp.2-6

より。

* 添付画像①のドットプロットは分かりやすくてよい。

* ②も箱ひげ図の使い方はひどい。こんなに小さなデータでしかも、単峰型であることに自信を持てない状況で箱ひげ図を使うべきではない。

* ③も不適切。 pic.twitter.com/mV0xMKkP0S

タグ：統計

posted at 18:29:32

#統計箱ひげ図は、基本的に、

「箱ひげ図で示される4つの区間に含まれるデータ中の値の個数は全部同じ」

と読みます。

データのサイズが小さくて、値全体の個数が数個の場合には、このようなシンプルな読み方では誤差が大きくなります。

そのような場合に箱ひげ図を使うべきではありません。 pic.twitter.com/RBMHt7njJp

タグ：統計

posted at 18:35:59

#統計箱ひげ図の元になる四分位数の定義は結構たくさんあります。定義のちょっとした違いで箱ひげ図の様子が変わってしまうような場合に箱ひげ図を使うのは非常にまずいです。

文科省版の四分位数の定義も独特。 twitter.com/genkuroki/stat...

タグ：統計

posted at 18:39:02

ʇɥƃıluooɯ ǝıʇɐs @tsatie

中学に降りたからなぁ... 中学の先生方がどれほど見て理解して啓蒙して下さる事か... twitter.com/genkuroki/stat...

タグ：

posted at 18:40:33

ʇɥƃıluooɯ ǝıʇɐs @tsatie

まぁそれ twitter.com/genkuroki/stat...

タグ：

posted at 18:41:05

二匹大介 @Yta8Ntion1FKvR0

@monachansdojo @temmusu_n @tomoak1n @sekibunnteisuu @math82307435 @togetter_jp あと、出来もしない「状況と数式が一致」を画策するがゆえに、パターンマッチング=暗記するしかない...となっているのでは...と思いますがね。

タグ：

posted at 18:41:39

#統計ところが、藤井良宜さんは rimse.or.jp/report/pdf/Rim... のp.5で添付画像のような箱ひげ図の使い方を授業で教えることを勧めています！

都道府県別のデータを使っているので、各「箱ひげ」に含まれる数値はたったの数個になってしまいます。さすがにこれはひどいです。 pic.twitter.com/40VjdUpEGG

タグ：統計

posted at 18:42:55

#統計中学生に数学を教えている人達は、この手の不適切な箱ひげ図の使用を勧める人たちに従わないように注意した方がよいと思いました。

可能ならば、この手の人達が進めている教え方を教育現場から批判するようになって欲しいと思います。

このままだと、ちょー算数の繰り返しになります！

タグ：統計

posted at 18:47:26

@Yta8Ntion1FKvR0 @monachansdojo @tomoak1n @sekibunnteisuu @math82307435 @togetter_jp #超算数全くねえ。式で場面を表せるという信念は、算数教育界の中心的教義なんですよ。子供が暗記解法にはしらないようになんてどこに書いてあるんですかねえ。むしろ、ふえるとなら足し算とか、指導の中にいっぱい子供を暗記解法に走らせがちなテクニックが含まれているんですから。

タグ：超算数

posted at 18:49:48

@Yta8Ntion1FKvR0 @monachansdojo @tomoak1n @sekibunnteisuu @math82307435 @togetter_jp #超算数しかも場面を表す式とやらは、項の順序を変えることで別の状況を表すとかいう、取り扱いの難しいものなんです。言葉や絵を描いて状況を表す訓練をした方がはるかに有益です。さらにいえばそういう訓練の代わりに式の順序を与えることで、子供から成長の機会を奪っているんです。

タグ：超算数

posted at 18:52:39

@Yta8Ntion1FKvR0 @monachansdojo @tomoak1n @sekibunnteisuu @math82307435 @togetter_jp #超算数テクニック主義を非難しつつtwitter.com/monachansdojo/...、掛け算の順序という小技や、場面を表す式と計算する式みたいな対立をむしろテクニック主義に対峙するものと考えているのが、もなちゃんの英語道場さんのよくわからないところですね。

タグ：超算数

posted at 18:55:35

#統計

藤井良宜さんは rimse.or.jp/report/pdf/Rim... のp.3にあるドットプロット(添付画像①)に対応するp.4で箱ひげ図(添付画像②)を示しています。

それらを比較すれば、箱ひげ図がどれだけ多くの情報を落としているかがよくわかります。続く pic.twitter.com/YZB3pkGc7f

タグ：統計

posted at 18:58:04

#統計

* 箱ひげ図ではデータのサイズが不明になる。サイズの小さなデータを扱っているという情報は非常に重要。

* ドットプロットは単峰型でない可能性もありそうなことを示しているが、箱ひげ図ではそういう構造は何も見えなくなる。

* 箱ひげ図では7,8,9が0人なことも分からなくなる。 pic.twitter.com/ZyoiQVVn6V

タグ：統計

posted at 18:58:05

#統計以下のリンク先では、藤井良宜さん達のお仲間に見える青山和裕さんが【箱ひげ図の箱の部分を母集団の中央値の50%信頼区間ととらえるような見方】が指導で取り入れられているなどと、トンデモない報告をしている場面を引用しています。

この手の傾向は、全く洒落にならないと思います。 twitter.com/genkuroki/stat...

タグ：統計

posted at 19:05:28

Nelmachine @Nelmachine

昔2chで大喜利やってた
「グラフにすればそんなに差はない」(2chはかなりネタ)
を真面目にやったもののようだ。 twitter.com/genkuroki/stat...

タグ：

posted at 19:10:31

何次のジョルダンブロックが何個で～っていう求め方、マスオさんのサイトでも軽く紹介されているけれど、これあんまり小さい行列で考えるとかえって分かりにくい気がするんだよな。

ジョルダン標準形の意味と求め方 manabitimes.jp/math/1307 pic.twitter.com/u1rSf4Wpvi

タグ：

posted at 19:10:37

#統計添付画像は

www.mext.go.jp/component/a_me...

のp.120より。これは現行の中2数学の学習指導要領の一部分。

私は特殊な場合にのみ便利な箱ひげ図が重要視されている理由がさっぱり分かりませんでした。

箱ひげ図についてろくに理解していない人達が頑張ったせいでこうなったのではないでしょうか？ pic.twitter.com/CQpl1eCtud

タグ：統計

posted at 19:13:49

#統計この辺については、最近、大久保さんが検索を始めたようです。以下のリンク先以外にも情報をツイッター上で大久保さんは紹介しています。

算数数学教育が専門の人達が、グラフの使い方さえろくに理解できていない状態で、中等教育での統計学教育を勧めている疑いがあります。この警告は重要！ twitter.com/ookubotact/sta...

タグ：統計

posted at 19:18:35

OokuboTact　大久保中二病中年 @OokuboTact

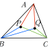
例えば、9次の正方行列で固有値が9重複しているとして、ジョルダン標準形が3,2,2,1,1次のジョルダンブロックに分割されるとする。
ここで
9-rank(J-λE)=5
は、ジョルダンブロックの個数になる。これはよくあるやつ。 pic.twitter.com/eWarZ8GJnr

タグ：

posted at 19:26:47

@genkuroki その後に見つけた情報です

twitter.com/OokuboTact/sta...

タグ：

posted at 19:31:44

こーた丼 @rental_math

箱ヒゲ図は用法要領を守って正しく使いましょう twitter.com/genkuroki/stat...

タグ：

posted at 19:32:55

次にrank(J-λE)とrank((J-λE)^2)の差を見ると、3減ってる。
もともと1次のジョルダンブロックだった場所はもう0になってて動かない。2次以上のジョルダンブロックだった場所のランクがひとつ減ったのだから、
rank(J-λE)-rank((J-λE)^2)=3
が、2次以上のジョルダンブロックの個数になる。 pic.twitter.com/5ZujtEuxQG

タグ：

posted at 19:35:38

相互リンク twitter.com/genkuroki/stat...

タグ：

posted at 19:38:04

#統計

 www.mext.go.jp/component/a_me...
のp.120より。中学校数学の学習指導要領の中2の部分の一部。

箱ひげ図は特殊な場合には非常に便利だが、普遍的に便利な道具ではないです。普遍性の低い道具を特別重視する学習指導要領の方針はまずいと思います。

おかしな人達の影響でこうなった可能性がある。 twitter.com/genkuroki/stat... pic.twitter.com/RgcBXdpcMO

タグ：統計

posted at 19:44:09

同様にrank((J-λE)^3)についても考えて、rank((J-λE)^2)との差が1だから、3次以上のジョルダンブロックの個数は1。
ここでランクが0になった(零行列になった)ので、最も大きいジョルダンブロックの次数が3であることが分かる。
最小多項式で最大のジョルダンブロックの次数が分かるっていうのはこれ。 pic.twitter.com/vTa83zfTYi

タグ：

posted at 19:45:09

あとは芋づる式に、ジョルダンブロックは全部で5個、2次以上が3個、3次以上が1個でこれが最大、というところからジョルダン標準形が分かる。
というのを整理したのが、最初に引用したこれで、佐武一郎『線型代数学』に載ってる解説とほぼ同じだと思う。たぶん。
manabitimes.jp/math/1307 pic.twitter.com/7R2fYUHKyb

タグ：

posted at 19:48:48

固有値λじゃないところが有ったら、まあそれはうまいこと消えます。

タグ：

posted at 19:51:08

高校数学の美しい物語 @mathelegant

マスオさん(@mathelegant)！！ぜひこの感じの解説をサイトに載せてください！！(僕が定期的に忘れてしまうので、思い出すのに便利だから)

タグ：

posted at 19:56:18

@bampaku ありがとうございます！しっかりとした解説とまではいきませんが、軽く追記させていただきました。

タグ：

posted at 21:31:35

@mathelegant ありがとうございます！はやい！このワンクッションが入るだけで、とても分かりやすくなりますね！

タグ：

posted at 21:33:20

#超算数同じ意見。

状況や場面を式で忠実に表現しなけれないけないという不合理な考え方を子供に押し付けるために、結果的に馬鹿げたパターンマッチ教育がはびこる。

しかも、算数教育界は戦前からずっとそういう方針。

その歴史をきちんと空瓶及使用済紙及腐敗食物的被廃棄物扱いする必要有り。 twitter.com/yta8ntion1fkvr...

タグ：超算数

posted at 21:40:20

増田聡 @smasuda