黒木玄 Gen Kuroki(@genkuroki)/2022年07月21日

ごまふあざらし(GomahuAzaras @MathSorcerer

コードを書く職業ならポジションはどうであれちゃんと書いて欲しい(・ω・｀)

タグ：

posted at 00:10:54

(・ω・｀)
めんどくさい場合はお金さえ積んで貰えば Python のスパゲッチースローライフコードを Julia に直しますよ.

タグ：

posted at 00:21:06

#超算数より進んで、算数教育界が掛順、足順の実在性をどこまで信じているかは、なお慎重な判断が必要です。公然と順序は実在するという人もいるし、発達段階とかファン・ヒーレを振り回して、子供はそう考えるという精神支配に及ぶ人もいます。

タグ：超算数

posted at 00:34:12

こどもを甲状腺がんの過剰診断から守る医師 @MKoujyo

#統計渡辺澄夫『ベイズ統計の理論と方法』の読者ならみんな知っている通り、通常の検定とベイズ因子(自由エネルギー)を比較する場合には、後者のn依存性に注意。

nを固定して、様子を見ようとするのはとてもまずいです。

タグ：統計

posted at 01:29:31

こどもを甲状腺がんの過剰診断から守る医師 @MKoujyo

NHKニュースででてきた、放射線によるものを否定しないで、過剰診断と言わないでの話ですが、放射線によるがんと考えている方の家族が自責の念に苛まれている動画を見ました。過剰診断の話は当事者を苦しめる話？

NHK 福島県のニュース www3.nhk.or.jp/lnews/fukushim... pic.twitter.com/h3VvNIO3mS

タグ：

posted at 05:17:34

インスタでも解説しています
www.instagram.com/p/CaotflFLcrz/

タグ：

posted at 05:17:35

囚人番号６ @F4EJ2Phantom

黒色火薬を作れないようにその材料を規制したら、別の部分で大変なことになるんだが。なんでこう、短絡的に物事を考えるかなぁ。先ずは穴だらけの警備体制のオペレーションリサーチによる是正からだろう。規制するなら🐎🦌でも出来るんだからさ。 twitter.com/hosono_54/stat...

タグ：

posted at 05:25:38

Erik Engheim @erikengheim

The creator of the #Odin programming language is doing an interesting analysis of the new language #Carbon being developed at #Google to replace C++.

Why not #Rust? Carbon has been made specifically to interface well with C++. Not a Rust goal.

www.youtube.com/watch?v=Z_8lV0...

タグ： Carbon Google Odin Rust

posted at 05:39:05

Erik Engheim @erikengheim

One thing that surprises me about a lot of Google languages is that none of them use similar syntax. Go, Dart and Carbon all pick rather arbitrarily different syntax. Surprised that a language from the same company doesn't try to be more syntactically similar.

タグ：

posted at 05:39:05

@hommedefer3 @CoveringNumber #統計個人的にミスリーディングな説明がある統計学入門の教科書や講義の情報を集めているので、

【尤度比検定以外は2回近似してるので、基本的には尤度比検定が好まれる】

のような奇妙な解説が書いてある教科書などを知っているなら、教えてくれるとうれしいです。

タグ：統計

posted at 06:59:21

@hommedefer3 @CoveringNumber #統計比率の検定や2×2の分割表の独立性検定では、スコア検定がお勧めです。

小標本の2×2の分割表での数値的確認によれば、対数尤度比検定だと過剰にP値が小さくなり易い場合が多かったです。私なら使わない。スコア検定(Pearsonのχ²検定)はかなり頑健でよい感じ。Waldは誤差が大き過ぎ。

タグ：統計

posted at 07:05:30

@hommedefer3 @CoveringNumber #統計当たり前の話ですが、n→∞での理想化された場合の数学的結果は、有限のnには適用できず、有限のnの場合には別の議論を追加する必要があります。

nが小さいときに、n→∞で漸近的に同値になる検定のどれが良さそうかは、コンピュータで実際に計算して確認すれば大体の所は分かります。

タグ：統計

posted at 07:09:56

@hommedefer3 @CoveringNumber #統計関連スレッド twitter.com/genkuroki/stat...

タグ：統計

posted at 07:15:59

@hommedefer3 @CoveringNumber #統計実践的には、統計ソフトが勝手に(デフォルトでは)Yatesに連続性補正をしている場合があるので要注意です。連続性補正を使うくらいなら、所謂正確検定をした方がよいと思います。

どうして連続性補正を使いたくなくなるかも、コンピュータで具体的な計算を大量に行うと納得し易い。

タグ：統計

posted at 07:21:02

@hommedefer3 @CoveringNumber #統計「漸近的に同値な検定のどれを使うか」よりも、「単一のP値の計算だけで判断することは止めるべきであること」の方が相対的にずっと重要で、「最低でも効果量の信頼区間くらいは計算しておくこと」も重要だと思います。 twitter.com/genkuroki/stat...

タグ：統計

posted at 07:38:18

#統計統計学入門の教科書には、違いの有無に関する検定のみを実行させる練習問題が沢山載っている場合があるのですが、「違いの有無に関する単独のP値の計算だけで判断してはいけない」という原則に反する教え方になっており、今後は廃棄されるべきスタイルだと思います。

journals.sagepub.com/doi/10.1177/02... twitter.com/genkuroki/stat...

タグ：統計

posted at 07:49:16

#統計

❌違いの有無に関する単独のP値の計算による検定のみを実行させる練習問題を沢山解かせる。
↓
↓代替案
↓
⭕️違いの有無に関する単独のP値を計算させるだけではなく、違いの大きさと向きを表すパラメータの信頼区間も計算してもらう。

そのとき、検定と信頼区間は表裏一体だと教える。

タグ：統計

posted at 07:54:02

#統計統計学ユーザー達の悪しき伝統のせいで、「有意差を出すか否か」のニ値的な判断を違いの有無に関する単独のP値の計算で行うことが普通に行われてしまっていることに、高等教育の側が合わせる必要はない全くないと思うし、むしろ、悪しき伝統の側に合わせることは問題のある教育になると思う。

タグ：統計

posted at 07:57:49

#統計高等教育(大学)でもこういう不安な状況なのに、高校の数学のカリキュラムに無理な感じで統計学ネタが押し込まれてしまったせいで、このスレッドに書いた問題はこれからの日本では悪化する可能性があると思います。

相当に不安な状態。

タグ：統計

posted at 08:00:05

@hommedefer3 @CoveringNumber 「2回近似している」という見方も誤りだと私は思います。 twitter.com/hommedefer3/st...

タグ：

posted at 08:03:30

#統計

点推定の結果だけを報告することはすでに非常識になっていると思う。

違いの有無に関する単独のP値のみを計算して二値的判断を下すことは、点推定の結果のみを報告することに似ていると思う。 twitter.com/genkuroki/stat...

タグ：統計

posted at 08:24:07

#統計関連 twitter.com/genkuroki/stat...

タグ：統計

posted at 08:24:24

#統計どう似ているか？

添付画像はデータとモデルとP値の計算法から得られるP値函数のグラフ。

①「効果はゼロ」という仮説の単独のP値は、P値函数のグラフとy軸の交点。

②効果の点推定はP値函数が最大になる効果パラメータの値。

どちらもP値函数全体の様子のほんの一部分でしかない。 pic.twitter.com/xCIquEHHFk

タグ：統計

posted at 08:38:37

#統計

①「効果はゼロ」という仮説の単独のP値

と

②効果の点推定

はどちらもデータの数値と統計モデルのパラメータ(効果)の値の整合性に関する情報のほんの一部分しか抽出していない。

たったそれだけの情報で重要な判断を下すのは馬鹿げていると思います。 pic.twitter.com/fI2gvex7Sz

タグ：統計

posted at 08:42:26

#統計 P値はモデルのパラメータ値とデータの数値の整合性の指標の1つです。

点推定は、データの数値との整合性の指標の値が最大のパラメータ値を求めること。

「効果はゼロ」という仮説のP値は、全てのパラメータ値に関する無数のP値の中の1つに過ぎない。 pic.twitter.com/PrDGka2xdI

タグ：統計

posted at 08:45:40

#統計 P値函数全体の様子が見えていれば、

①点推定→x軸上の一点
②「効果はゼロ」という仮説のP値→y軸上の一点

のどちらも軸上の一点の情報を取り出しているに過ぎない。

それだけの情報だと真っ当な判断はできそうもない。

こういう話については最新の論文 journals.sagepub.com/doi/10.1177/02... を参照。 pic.twitter.com/xFuERm6xXl

タグ：統計

posted at 08:50:27

#統計添付スクショは論文

journals.sagepub.com/doi/10.1177/02...

の最初の部分。

①P値は数値を報告するべき。有意水準未満かどうかだけを報告するべきではない。

②「統計的に有意」という言い方を使うことは全面的に止めるべき。

③信頼区間も報告するべき。

④以上だけでは足りない。続く pic.twitter.com/BuwWjTv22g

タグ：統計

posted at 13:10:31

#統計続き

④続き。「効果無し」という帰無仮説に関する単独のP値だけでは不十分である。これ大事。

以上の①②③のような提案が「効果無し」という帰無仮説単独のP値のみを言及しているとみなされる限り、それらはミスリーディング(誤解誘導的)である。 pic.twitter.com/sSKbA7SlBV

タグ：統計

posted at 13:16:18

#統計論文 journals.sagepub.com/doi/10.1177/02... を読むと、以下のリンク先での教え方の代替案(練習問題では、「効果無し」の帰無仮説単独のP値だけではなく、効果の信頼区間も同時に計算させるように注意する)であっても、まだ有害な結果を招くことを心配する必要があります。 twitter.com/genkuroki/stat...

タグ：統計

posted at 13:20:23

#統計心配するべきことは

(1) 「効果=0」という型の仮説のみを検定できると誤解させてしまうかもしれない。実際には「効果=○○」(○○は任意の数値)のより一般的な型の仮説のP値も計算できる。

(2) 信頼区間上の各点には有意水準以上の値のP値が対応していることに気付けなくする心配がある。

タグ：統計

posted at 13:31:27

#統計効果の信頼区間の定義は、「効果=a」という仮説のP値が有意水準以上になる値a全体の集合なのですが、統計学入門の教科書にこのクリアな信頼区間の定義が書いてあることは稀で、P値や検定と無関係に区間を計算するやり方だけが説明されていたりすることが多い。

効果以外のパラメータでも同様。

タグ：統計

posted at 13:35:55

#統計

△ 練習問題では、「効果無し」の帰無仮説単独のP値だけではなく、効果の信頼区間も同時に計算させるようにする。
↓
↓さらなる改善
↓
⭕️ 任意の数値aに関する「効果=a」という仮説のP値を計算して、「効果=a」という仮説とデータの数値の整合性の指標として利用できることを強調する。

タグ：統計

posted at 13:43:05

#統計そして、信頼区間をP値を使って定義してしまえば、信頼区間は「データの数値との整合性が無さ過ぎる」と判定されずに済むパラメータ値全体の集合であることが明確になり、信頼区間を実践的にどのように使えばよいかもクリアになります。

タグ：統計

posted at 13:46:26

#統計「頻度論vs.ベイズ」的な有害な言説の宣伝者達は「頻度論では『効果無し』の帰無仮説を否定はできるが、肯定することはできない」のように言います。

しかし、それは単に「効果=0」のP値しか計算しない状況を想定しているから、妙な所を強調しているに過ぎない。無知が原因の不適切な強調。

タグ：統計

posted at 13:55:45

#統計 |a|≥ε のとき「効果=a」という仮説のP値が有意水準以上になるならば、有意水準の危険率の下で、データの数値と整合性が無さ過ぎると判定されずに済む効果の値の絶対値はε未満であることになります。

ぴったり「効果=0」であるという仮説について判定下せないが、εで幅を持たせれば可能になる。

タグ：統計

posted at 14:00:55

#統計これは、効果の信頼区間が0±εの中におさまっている場合と同じことになっています。

信頼区間を使ってできることをきちんと説明せずに、「頻度論では『効果無し』の帰無仮説を否定はできるが、肯定することはできない」のように言うことは、悪質な印象操作になっており、相当に問題がある。

タグ：統計

posted at 14:04:00

#統計そして、最新の論文 journals.sagepub.com/doi/10.1177/02... で解説されているようなことは、相当に前から世界中でよく読まれているロスマンさん達の疫学の教科書にも書かれていることです。

そういう類のことを勉強せずに「頻度論ガー！」と言うのは非常にみっともないと思う。

タグ：統計

posted at 14:06:39

#統計まあ、それはそうとして、統計学の正しい使い方に関する議論をずっと行なっている専門家達のあいだで、

⭕️「統計的に有意」というフレーズの使用を全面的に避けるべきである(②の部分)

という点については、コンセンサスが得られているように見えることは注目に値すると思いました。 twitter.com/genkuroki/stat...

タグ：統計

posted at 14:12:18

#統計まだ考えがまとまっていないのですが、

(a) データの数値とモデルのパラメータ値の整合性の指標

の1つとしてのP値だけを扱うだけではなく、

(b) データの数値とモデルによる予測の整合性の指標

も定義できる場合があることも重要だと思います。例えば、線形回帰の予測区間を与えるP値函数。

タグ：統計

posted at 14:28:32

#統計データの数値と

(a) モデルのパラメータ値
(b) モデルによる予測

の整合性の様子を見るために、何か指標を用意して利用したい。

これはP値を使う方法に限らない要求で、ベイズ統計では

(a) パラメータの事後分布
(b) 予測分布のP値やAIC, WAIC, ...

の話が対応していると思う。考え中。

タグ：統計

posted at 14:32:09

#統計ベイズ統計と言われれば、周辺尤度比(所謂ベイズ因子(Bayes factor))、もしくは対数を取って、対数周辺尤度比を使う話と通常のP値の関係については以下のリンク先を参照。 twitter.com/genkuroki/stat...

タグ：統計

posted at 14:41:44

#統計

通常のP値(もしくは近似的にχ²分布に従う検定統計量)

と

ベイズ因子=周辺尤度比(もしくは対数周辺尤度比)

を数値的に比較する場合には、それらの漸近挙動の違いから、標本サイズnを動かして様子を見る必要があります。←これ大事

以下は

github.com/genkuroki/publ...

のスクショ。 pic.twitter.com/j4X3NDDtcR

タグ：統計

posted at 14:45:52

#統計

信頼区間=与えられた有意水準と統計モデルの下でデータの数値と整合性が無さ過ぎると判定されずに済むパラメータ値全体の集合

という話については、以下のリンク先で紹介した有名な教科書に書いてあるとみなせます。 twitter.com/genkuroki/stat...

タグ：統計

posted at 14:50:05

#統計ベイズ因子 < 1 という条件で真のモデルの選択に失敗する確率と有意水準α_nを適当にnとともに単調減少するようにしたときのχ²検定での同確率を重ねてプロット。

ほぼぴったり重なっています！

問題：これは何を意味するか？続く

github.com/genkuroki/publ... pic.twitter.com/cHJxJ9UfWM

タグ：統計

posted at 15:42:49

#統計ベイズ因子を使った仮説の選択は、通常のP値を使ってもほぼ同じことをできることを以下のグラフは示しています。

「頻度論vs.ベイズ主義」という悪しき言説を宣伝している人たちの言い分とは違って、ベイズ因子と通常のP値は水と油ではありません。続く

github.com/genkuroki/publ... pic.twitter.com/cNGe5yVBzl

タグ：統計

posted at 15:46:24

#統計それらの漸近挙動の間の関係を使えば、ベイズ因子を使った検定は、n→∞で有意水準を単調に0に収束させるような設定を具体的に書き下すことによって、通常のP値を使った検定でシミュレートできます。

実際にできていることの証拠が以下のグラフ。 pic.twitter.com/USKDeP36WS

タグ：統計

posted at 15:48:50

#統計ベイズ因子もしくは周辺尤度比もしくは対数周辺尤度比を使ったモデル選択は、n→∞で真のモデルを確率1で選択するようになることを、ベイズ統計の優れた点だと単に言っている人達は、有意水準をn→∞で0に近付けることを単に利点だと主張しているだけで、それには欠点があることに無頓着です。

タグ：統計

posted at 15:52:06

Yuki Nagai @cometscome_phys

報告フォームも用意しました(githubのissue)
github.com/cometscome/Yuk...

タグ：

posted at 15:52:54

#統計統計学入門を終えた人なら誰でも有意水準を極小にすると検出力も極小になるという欠点があることを知っています。

結局のところ、あらゆる点で優れている統計学的方法など存在せず、常にトレードオフで考えなければいけない、という穏当な結論に落ち着くのだと思います。

タグ：統計

posted at 15:54:14

#統計この手の話(ベイズ因子と通常の検定の比較や主義に基く統計学がダメであること)については、渡辺澄夫『ベイズ統計の理論と方法』に実質的に既に書かれていることに過ぎません。

タグ：統計

posted at 15:56:48

#統計渡辺澄夫『ベイズ統計の理論と方法』は色々フェアに書かれている良い本だと思います。

ベイズ法が優れている理由の合理的な説明もその第4章にあります。

タグ：統計

posted at 15:59:53

#統計【統計検定でそう教わって】

多分、そう教わったのは、p_A - p_B = 0 という仮説の検定の場合についてなので、大丈夫な可能性が高いと思いました。

私の指摘は、Δ≠0の場合のp_A - p_B = Δ という仮説の検定法としては間違っているということです。こちらは信頼区間の話に関係しています。 twitter.com/rx_magazine/st...

タグ：統計

posted at 16:16:01

#統計それでは、p_A - p_B = Δ という仮説の検定や信頼区間をどうすればよいのかについては、Zou-Donner 2004を紹介して実装例も示しています。

この手の話題では、単に誤りを指摘するだけではなく、代替案を文献に引用とともに示すことが大事だと思います。

github.com/genkuroki/publ... pic.twitter.com/lLPK1BvAm9

タグ：統計

posted at 16:22:21

祥太(8.12 C102 1日目東ヌ4 @shota_

#統計 Zou-Donner 2004 doi.org/10.1016/j.cct.... の信頼区間と対応するP値函数の実装では、添付画像のコードを見ればわかるように、atanh (arc tanh)が本質的な役目を果たしています。

統計学の文脈では arc tanhとtanh による変換はFisherのz変換と呼ばれている。

github.com/genkuroki/publ... pic.twitter.com/LWajrfybgQ

タグ：統計

posted at 16:26:54

既存宗教に入ってればカルトに強くなるかと言えば全然そんなことはない。

でなきゃカトリック中央協議会やカトリック司教団が教会にカルトへの注意喚起を貼り出したりしないもの。

人は簡単に騙される。

タグ：

posted at 16:36:39

#超算数
読了　気になる点を書いておく
twitter.com/IwanamiNatura/...

タグ：超算数

posted at 16:49:26

#超算数　この教員の教え方は駄目だろう。正三角形が二等辺三角形であることを理解している点は、陰山英男よりはましではあるが。

陰山英男は「正方形は長方形ではない」という認識で論外。sumatome.com/su/10866206181... pic.twitter.com/btKDvJWhea

タグ：超算数

posted at 16:52:18

#超算数
筆者は、

最初から正三角形は二等辺三角形であると教えないこと

に理解を示すが、

それと

正三角形は二等辺三角形ではないと教える
正三角形を指して「二等辺三角形」と答えた生徒に「間違いです」と言う

こととは雲泥の差がある。 pic.twitter.com/s18sdrb9Up

タグ：超算数

posted at 16:53:46

#超算数　

第5章　かける数とかけられる数は同じだった

結論から言うと、かけ算の順序問題についてはほとんど書かれていない。筆者はこれが議論になっていることは認識したうえで、敢えてそこには触れないで、「かける数」「かけられる数」という用語が分かりにくいと言うようなことを言っている。 pic.twitter.com/cBdsgBWRH0

タグ：超算数

posted at 17:02:17

#超算数　

　要するに、「座る人」「座る椅子」はどちらも、動詞「座る」の連体形+名詞　の形になっているけど、
人が椅子に座るのであって、その逆ではない。

　椅子が座る訳じゃない、人の上に座るということは普通はない、という常識で「座る人」「座る椅子」の意味を解釈している。

タグ：超算数

posted at 17:05:14

#超算数　　
「書くものがない」という場合、筆記用具がないのか、紙がないのか、ネタがないのかは文脈次第。

本では、「パンケーキにシロップをかける」を例にして、パンケーキ、シロップ、どちらも「かけるもの」になり得ると言う。

タグ：超算数

posted at 17:09:02

#超算数
そりゃそうだけど、そこはかけ算順序問題の本質じゃない。

「かける数」「かけられる数」を教えることを含めて問題視されているのだが、

巷間では「掛け算順序問題」は、「どちらもマルにしろ」という主張に思われているようだ。

これは、こちらの側の宣伝の失敗である。

タグ：超算数

posted at 17:13:18

#統計以下のスレッドの内容を前提にすると、

粕谷英一『生物学を学ぶ人のための統計のはなし～きみにも出せる有意差～』

の副題の「きみにも出せる有意差」は非常にまずい考え方だということになると思います。

この本には良いことも沢山書いてあるので、おかしな所を全部訂正したものが欲しい。 twitter.com/genkuroki/stat...

タグ：統計

posted at 17:38:56

#統計「きみにも出せる有意差」は、以下のスレッドの文脈では、「違いがない」という仮説のP値のみを計算して決着をつけることで、違いをどのように測るかに頓着しないので、パラメトリック検定の代替品としてノンパラメトリック検定も無批判に自由に使える設定になっています。これはまずいと思う。 twitter.com/genkuroki/stat...

タグ：統計

posted at 17:44:28

#統計現実世界での統計学の応用では、単に違いがあるか否かではなく、「違いとして現れる効果の大きさと向きがどうなっているか」が重要なので、違いをどのような指標で測るかは非常に重要です。

タグ：統計

posted at 17:46:48

#統計例えば、違いを「平均の差」で測ることにし、Welchのt検定とそれと表裏一体の平均の差の信頼区間を使う場合と、違いの測り方がそれとは全然違うノンパラメトリック検定を使う場合では、全然違うことをやっているとみなされる必要があります。

タグ：統計

posted at 17:49:21

#統計そういう違いの測り方について完全に無頓着になって、単に「有意差を出したい」という理由で、十分な考慮無しに、ノンパラメトリック検定をWelchのt検定などの代替品とみなすことは、非常によろしくない統計学の使い方をしていると思います。

タグ：統計

posted at 17:51:47

#統計しかし現実には、「効果をどのように測るか」と直接的に関係がある検定法の選択において、単に「有意差を出せればよい」という常識的な意味でおよそ科学的とはとても言えそうもない態度で、パラメトリック検定の代替品としてノンパラメトリック検定を使っても良いかのように思われていたりする。

タグ：統計

posted at 17:55:24

#統計そういう常識的に考えて科学的とは言えない態度が、まるで科学的であるかのように思われている場合があることは、我々の次の世代の人たちのことを考えると憂慮するべきことなのではないかと思います。

こういうことを言う人達を普通に見かけない点もかなり不安な感じ。

タグ：統計

posted at 17:58:08

#統計ついでに述べておくと、Welchのt検定の方法は、中心極限定理が十分効いていて、2つの母集団のサンプルの標本平均の分布が正規分布で近似できる状況であればそう悪くない誤差で使用可能です。

2つの母集団分布が正規分布になっていなくても、そういう場合には使用可能です。

タグ：統計

posted at 18:04:13

#統計 2つの群の平均の差に関するStudentのt検定も同様の理由で、正規母集団の仮定抜きに使えます。ただし、使用可能条件がWelchのt検定よりも厳しくなっていて、中心極限定理による近似の他に、

(1) 等分散
(2) 等標本サイズ

の少なくともどちらか片方の条件が必要です。

タグ：統計

posted at 18:08:45

#統計だから、そもそも「パラメトリック検定」「ノンパラメトリック検定」という用語を、母集団分布が例えば正規分布であることを仮定した場合の検定であるか否かを意味するというニュアンスで使っている傾向自体が、基本的な所でミスリーディングを引き起こしているわけです。

タグ：統計

posted at 18:10:56

нал Д’ал дере @nal_dal_dere

#統計以下のリンク先のようなことは、教科書での説明では見たことがなく、私が地道に自分で確認して得たことです。

書いてある教科書があれば引用したいと思うので、知っている人がいれば教えて下さい。論文でもよいです。 twitter.com/genkuroki/stat...

タグ：統計

posted at 18:13:06

@genkuroki 生物学屋あるあるですね…

タグ：

posted at 18:14:17

#統計私は、学生時代から「教科書や論文に書いてあるという理由で正しいと判断してはいけない」というスタイルが普通の文化圏でずっと過ごしているので、既存の文献に頼らずに全部自分で再構成することは「普通の仕事」なのですが、これ、慣れているとはいえ、滅茶苦茶しんどい作業です。

タグ：統計

posted at 18:19:25

#統計普通の人が手に取れる教科書に、適切な根拠があること(ただし、有名な教科書や査読論文に書いてあるという事実自体は正しいことの根拠にはならない)が書いてあってほしいと思います。

タグ：統計

posted at 18:19:26

#統計改善するべき点

❌有意差を出すために、違いの測り方が異なるような検定であっても代わりに使ってよいことにする。

⭕️「違いをどのような指標で測りたいときにどの検定を使うか」の形式で検定法を分類して解説し、さらに「違いの指標=a」という仮説のP値も定義する。 twitter.com/genkuroki/stat...

タグ：統計

posted at 18:28:24

#統計改善するべき点

2×2の分割表の独立性検定について、

❌χ²検定はFisher検定の近似なので、標本サイズが小さい場合にはFisher検定を使うべきだと説明する。
↓
⭕️Fishet検定は特に標本サイズが小さい場合に保守的な方向に大きな誤差を持つ。独立性検定法の使い分けをトレードオフで説明する。

タグ：統計

posted at 18:31:41

#統計改善するべき点

❌最尤法は「手持ちのデータが得られる確率がいちばん高くなるような母集団の状態がいちばんありそうだと考えること」(p.124)と説明。

⭕️最尤法は「データと同じ数値がモデル内で得られる確率が最大になるパラメータ値を求めて、モデルをデータの数値にフィットさせること」

タグ：統計

posted at 18:39:36

#統計例えば、サイコロを3回振ったら3回続けて偶数の目が出たとき、ベルヌーイ分布モデルまたは二項分布モデルの最尤法では、偶数の目が出る確率を意味するパラメータ値を1にすることになる。

しかし、それは単にモデルのパラメータ値をデータに合わせて調節しただけです。それ以上の意味はない。

タグ：統計

posted at 18:42:29

#統計それなのに、「偶数の目が出る確率は1であることがいちばんありそうだ」などと思うことは、賭け事では負け組になることが確定するレベルで極めて不合理な考え方だと思います。

こういう常識レベルで明らかにおかしな説明はできるだけ排除して行きたい。

タグ：統計

posted at 18:47:46

#統計多分、この手の話でもっとも重要なことは、現実の母集団分布と統計モデルを明瞭に区別することだと思います。

そして、最尤法の類は、パラメータを調節してデータにモデルをフィットさせているだけなので、その結果が「いちばんありそうだ」とは決して考えないことです。

タグ：統計

posted at 18:51:25

#統計最尤法などの点推定の結果だけではなく、区間推定(信頼区間)も報告することが常識的になっていると思う。

P値函数と「効果=0」のP値と点推定の関係
↓ pic.twitter.com/TocCtrPevJ

タグ：統計

posted at 18:53:50

#統計 1つ前のツイートの添付画像と同じような図を、P値函数を尤度函数やBayes統計での事後分布に置き換えても書けます。

P値函数、尤度函数、事後分布はどれも、モデルのパラメータ値とデータの数値の整合性の情報を持っているとみなせます。

タグ：統計

posted at 18:56:03

нал Д’ал дере @nal_dal_dere

#統計そんな方針で、P値や信頼区間や最尤法などなどについてより「現代的」な解説と、粕谷さんの本の中の実践的に有益な事柄の解説部分をうまく融和した教科書があると良いと思いました。

タグ：統計

posted at 18:58:26

нал Д’ал дере @nal_dal_dere

@genkuroki ちょうど学部の卒研でWelchのt検定でデータを検定したんです。院試の時に面接で卒論のデータは何で検定しましたかと言われたので、こう言うデータでしたのでt検定ですと答えたんですが、それ以上の突っ込みはありませんでした。
入学すると、一般化線形モデルを使っておけばとりあえず大丈夫という教育

タグ：

posted at 19:15:40

@genkuroki どういう集団にどういう指標を適用すれば、どういう性質の違いがあると言えるのか？という統計の基本的なスタンスが共有されていない感じでした。

タグ：

posted at 19:17:28

ちょこ @sos_uts

やっぱりjuliaのほうが好き

タグ：

posted at 19:47:30

永井 @HNagai1108

Rで書かれたお手本を参考に、レプリカ交換をJuliaで実装した

タグ：

posted at 20:45:18

永井 @HNagai1108

あとは並列化したいな

タグ：

posted at 20:45:44

ゆうちょ @yucho147

手を洗う救急医Taka @mph_for_doctors

「Python3.11はやーい」ってツイートに「素晴らしい進歩だが、まだまだっすな」ってjuliaのスクショ送りつけるクソリプを見つけたw

タグ：

posted at 21:48:44

日経新聞エラい塩野義の新薬を推しますね。

「緊急承認制度は米国の緊急使用許可（EUA）を手本にした。」

とありますが、現状のデータで🇺🇸のEUAは絶対通らないと思いますよ。 twitter.com/nikkei/status/...

タグ：

posted at 21:58:29

@sekibunnteisuu @ken1maeda #超算数これは私の感想(添付画像の赤字部分)。

①1あたり量×幾つ分の順序ではなく、幾つ分×1あたり量の順序でも合理的であることの宣言がない。

②4×6の解釈は多彩であり、1つに固定しようとする圧力をかけること自体が教育にとって有害。まさにそれをやろうとしているように見える。 pic.twitter.com/5Wo3kiOcO1

タグ：超算数

posted at 21:59:44

#統計実質的に有意水準α_nをn→∞でα_n→0とする検定と同値なベイズ検定と通常の有意水準5%の検定のパワーをプロットしてみました。帰無仮説はp=p₀=0.5で真のpが0.6と0.55の場合。

ベイズ検定での閾値は1なので最強化されているが、通常の検定より検出力が弱い。

トレードオフの問題。 pic.twitter.com/9Qf8pakG2F

タグ：統計

posted at 22:19:34

#統計限られたデータから引き出せる情報も限られているので、ある程度以上合理的な方法どうしを比較すると、ほぼ常に「あちらを改善すると、こちらが悪化する」のようなトレードオフの問題が生じる。

各種のトレードオフに関する情報が広まっていた方が、みんな適切な方法を採用し易くなると思う。

タグ：統計

posted at 22:23:24

ダラコ @daaaaa_rakong

おぉう…この地元民放と全国民放の違い、知らなかった。罪深い話だ。 twitter.com/sonohennokuma/... pic.twitter.com/wnboUynSZF

タグ：

posted at 23:04:03

ダラコ @daaaaa_rakong

個人的にはここがすごく興味深かった。どうして健康状態がよいと、そうでない人より不安が有意に低いんだろう。 pic.twitter.com/Ca66wik34F

タグ：

posted at 23:07:23

としゅきー™ @toshchy

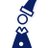
OEISのA143742(oeis.org/A143742)に載っている20個の自然数

　1, 2, 3, 9, ..., 5812827, 7110201

を初項として，それぞれのジャグラー数列(Juggler sequence)を計算した結果．全て1に収束．

(テキストデータ→toshchy.com/research/juggl...) pic.twitter.com/sC2dinzXmE

タグ：

posted at 23:08:03

としゅきー™ @toshchy

172376626(1億7237万6626)以下の全ての自然数についてジャグラー数列を計算し，

・数列中に出現する最大項が最も大きいもの
・1に収束するまでに必要なステップ数が最も多いもの

それぞれのTOP20を集計した結果．全て1に収束．

テキストデータ↓
toshchy.com/research/juggl...
toshchy.com/research/juggl... pic.twitter.com/EdlvMIDhxf

タグ：

posted at 23:10:26

#超算数 1971年使用開始の教科書は、現代化(1968年)指導要領における最初の教科書です。指導要領は同年4月施行を謳っている。集合がどうとか理屈っぽい基礎を持っていますが、1年生だからか限りなくシンプルですね。 twitter.com/sekibunnteisuu...

タグ：超算数

posted at 23:23:09

残り5件のツイートを見る

@kuri_kurita

朝日新聞がしきりに

「金融緩和やめろ」
「利上げしろ」

と庶民の利益に反する主張を叫んで煽ってますが、さすが緊縮カルトのプロパガンダ紙。

digital.asahi.com/sp/articles/AS...

タグ：

posted at 23:23:53

としゅきー™ @toshchy

a[0]=172376627 は，a[90]の計算結果が Inf になって失敗．

a[87]=1.027479e+133235443
a[88]=3.293515e+199853164
a[89]=5.977085e+299779746
a[90]=Inf

a[90]の概算オーダーは1.0e+449669619．このあたりがJulia(1.7.3)のBigFloat型の限界っぽい．無念～．

タグ：

posted at 23:26:04

#超算数ところで、その次の指導要領は1977年に告示され、81年4月に施行されました。教科書データベースには使用期間が1980年から82年の算数教科書が学校図書から出たことが記録されています。80年代から足し算の意味が強調されるようになったとの印象は、移行措置を含む1977年指導要領の影響と整合。 pic.twitter.com/EZEgbVpCEi

タグ：超算数

posted at 23:30:25

#超算数もちろん足し算の順序は守屋操も認めていたtwitter.com/temmusu_n/stat...。戦前の資料は未見だが、あっても不思議ではない。また、現代化精算(1977年)指導要領の期限切れ以降も意味説は亢進し、現代になって猖獗を極める。ただし、この時なにか特異的なことが起こった可能性は高い。

タグ：超算数

posted at 23:37:25