黒木玄 Gen Kuroki(@genkuroki)/2017年11月/Page 6

近藤誠はなぜ平然としていられるのか

タグ：

posted at 00:41:21

事実上近藤誠に殺されたと言っても過言ではないケースは膨大にあるのではないのだろうか

タグ：

posted at 00:44:33

こういうインチキ団体に引っかからないように気をつけてね twitter.com/opkodomotachi/...

タグ：

posted at 00:46:04

招き猫 @kyounoowari

このイアン・ブレマーのインタビューは重いなぁ
欧米で自由民主主義が機能しなくなっている中で日本だけが自由民主主義モデルが機能している
安倍総理がベタぼめされているというより、欧米の政治情勢が機能不全に陥った中で、日本だけが唯一の救いのようにブレマーは見ている。 twitter.com/bloombergjapan...

タグ：

posted at 01:01:08

Viral B. Shah @Viral_B_Shah

Simply amazing what @SimonDanisch can do with generic programming and specialization in #julialang twitter.com/SimonDanisch/s...

タグ： julialang

posted at 02:44:26

Viral B. Shah @Viral_B_Shah

うさぎ林檎＠ししょーPPMP @usg_ringo

@SimonDanisch Looks like the GPU stuff in #julialang is quickly reaching ahead of everything else! Kudos

タグ： julialang

posted at 02:45:32

うさぎ林檎＠ししょーPPMP @usg_ringo

こういう連中も近藤誠氏を肥大させたのよな。「２０１２年に発売された「医者に殺されない４７の心得」は１０８万部のベストセラー」「２０１２年に菊池寛賞」・2014年｜近藤誠「がんは切るな見つけるな」異端の医師｜金スマ tvmatome.net/archives/979

タグ：

posted at 09:46:03

オーストラリアのビクトリア州消費者局が「出版社は著者が虚偽を書いてないか確認する責任」で著者だけでなく出版社に罰金３万ドル払わせてる事例があるんです。この手の問題は出版社側の責任は決して小さくないですもんね。
twitter.com/usg_ringo/stat... twitter.com/zorotto_BJ/sta...

タグ：

posted at 09:55:25

#統計 #数楽以下のリンク先のツイートがたくさんRTされている。赤池情報量基準AICの導出には渡辺澄夫さんが書いた教科書がおすすめ。背景の数楽の簡潔な説明が
watanabe-www.math.dis.titech.ac.jp/users/swatanab...
にある。続く

twitter.com/genkuroki/stat...

タグ：数楽統計

posted at 10:05:26

#数楽 AICの導出まで理解するのは計算が面倒なのですが、AICがどのような条件のもとで何の推定量になっているかやAICが予測分布の精度の相対比較に使えることまでを知ることはそう面倒なことではないと思う。
watanabe-www.math.dis.titech.ac.jp/users/swatanab...

タグ：数楽

posted at 10:08:55

#数楽 watanabe-www.math.dis.titech.ac.jp/users/swatanab... より引用【この問題はBernstein-Sato の b 関数の概念の無限次元化に相当すると思われるので数学的にも重要であると感じられるが、今のところ、容易ではないように思われる。（注意４終）】

タグ：数楽

posted at 10:11:16

#数楽 watanabe-www.math.dis.titech.ac.jp/users/swatanab... 【超関数の位相は関数空間の位相としては最も緩いものであり、ベイズ推測は超関数の位相で学習することを意味している。事前分布は超関数を考えるための相手となる基礎関数に相当する。】事前分布はテストファンクションに対応。

タグ：数楽

posted at 10:13:06

#数楽同論説より【ゲルファント・シーロフの有名な超関数論に関する教科書には（そのころは、まだ特異点解消定理もベルンシュタイン・佐藤の多項式も知られていなかった）、対数閾値に関する具体的計算が繰り広げられている。】"Generalized Functions"は特殊函数の本(笑)

タグ：数楽

posted at 10:18:07

#数楽同論説より【1970年にAtiyahが特異点解消定理に基づいて対数閾値に相当する概念が存在することを示し、偏微分方程式の基本解の存在を証明～。対数閾値は極小モデル理論において重要な位置を占めている[7]～振動積分の漸近展開に現れることを示したのはVarcenko～[6]】

タグ：数楽

posted at 10:21:02

#数楽引用続【まったく知らない分野を調べるのは大変であったし、いまでもまだ大変である。～特異点解消定理やベルンシュタイン・佐藤の多項式の存在は、学習の過程を定めているのは何であるのか、を理解する上で、重要な情報を与えてくれた（注意７終）】数理研にいたことが大きかったのだと思う。

タグ：数楽

posted at 10:23:49

#数楽 watanabe-www.math.dis.titech.ac.jp/users/swatanab... 【しかしながら「物理学の問題は観測量の代数的構造に自然な表現を与えることで解決される」という基本は、本研究においても成り立っていた。誠に不思議なことである。（注意10終）。】

タグ：数楽

posted at 10:27:22

#数楽赤池情報量基準AICの定義はパラメーター数dの確率モデルの最尤法における

AIC=-2log(最大尤度) + 2d

なのですが、2dの項の真の意味を追求して行ったら、代数幾何における特異点解消と代数解析におけるb函数の理論がもろに関係していたという話です。

タグ：数楽

posted at 10:33:02

砂___の___女 @vecchio_ciao

この人は #掛算の件でもアレなことを言っていた人。 .@AS_Insects さんの「とある高校教師さんとの文科省・内閣府統計についてのやりとりまとめ」をお気に入りにしました。 togetter.com/li/1169029

タグ：掛算

posted at 10:46:11

ITAL @ITAL_

米村歩@日本一残業の少ないIT企業社長 @yonemura2006

.@vecchio_ciao さんのコメント「この人は #掛算の件でもアレなことを言っていた人。」にいいね！しました。 togetter.com/li/1169029#c43...

タグ：掛算

posted at 11:05:50

プログラマー志望の学生の方は、面接の時に「仕事の時にスーツ着用は義務付けられていますか」と聞いてみましょう。プログラマーにスーツ着用が義務付けられていたらその会社はやめておいた方が良いかと。こんなこと言うとスーツ着用義務の開発会社から怒られそうですが本当のことなので言いました。ｗ

タグ：

posted at 11:17:53

#数楽 watanabe-www.math.dis.titech.ac.jp/users/swatanab... から引用。特異モデルの場合には【統計量を「サンプルからパラメータへの写像」と定義するのは自然でない。最尤推定量は漸近有効でも漸近正規でも漸近不偏でもない。AIC, BIC, MDL などは、意味を持たない。】

タグ：数楽

posted at 11:25:10

#数楽実際に有限のサンプルサイズで数値計算すると、Fisher情報行列が退化するパラメーター直上ではなく、そのすぐそばのパラメーターに対応する確率分布でサンプルを生成した場合にも、正則モデルとみなさない方が良いことがわかる。続く

タグ：数楽

posted at 11:31:48

かなか @kanakanaka_a

逆数を問う問題。
私「逆数の意味は？」
子「その数にかけると1になる数」
私「5/2の逆数は？」
子「2/5」
私「この解き方を書く意味は？」
子「意味っていうかそう書かないと怒られるから…」
先生『VERY GOOD!!』 #超算数 pic.twitter.com/PfBQJVJKnC

タグ：超算数

posted at 11:32:14

#数楽 Fisher情報行列が退化しているパラメーター全体の測度はゼロなので、厳密な意味でモデルが特異になることはないと考えられるが、サンプルサイズに対応する精度では特異モデルになっているとみなすべき場合があることが珍しくないことが実際に数値計算するとわかる。

タグ：数楽

posted at 11:38:56

#数楽「Fisher情報行列が退化しているパラメーター全体の測度はゼロなので、確率モデルが特異になることはないと思ってよい」という考え方は非現実的であり、実用に適さない。現実には近似的に特異モデルとみなすべき状況が珍しくない。

タグ：数楽

posted at 11:41:43

#数楽証拠

nbviewer.jupyter.org/gist/genkuroki...
1次元混合正規分布モデルの最尤法とベイズ法による推定例(サンプルサイズ2^5)

尤度函数の台が特異点(Fisher情報行列が退化する点)の周囲に集中した形をしており、近似的に特異モデルとみなすべき状況になっている。

タグ：数楽

posted at 11:45:22

#数楽 MCMC(#JuliaLang を使用)で近似的に求めた事後分布posteriorと尤度函数likelihood functionの形はほぼ同じ。それらの台は特異点集合ab=0の周囲に集中している。 pic.twitter.com/LdJBFhlE8s

タグ：数楽

posted at 11:49:54

積分定数 @sekibunnteisuu

#超算数　 #絶対値
p11　
「ー３の絶対値を答えよ」　解答「３」
「絶対値が５である数を答えよ」　解答「＋５，－５」

３と＋３は全く同じ、５と＋５は全く同じだから、嘘は書いていない。
でも、この書き方はミスリーディング

タグ：絶対値超算数

posted at 11:50:32

積分定数 @sekibunnteisuu

#超算数　 #絶対値
中学数学の問題集・教科書などで、「絶対値を求めよ」の正解例が、符号付きになっているようなものがあったら知らせて欲しい。

タグ：絶対値超算数

posted at 11:52:13

#数楽 Bayesian meanは事後分布の平均のこと。ただし事後分布の平均をベイズ推定の推定結果とみなすのは誤り。ベイズ推定の推定結果は事後分布で確率モデルを平均して得られる予測分布。

「パラメーターの推定」は特異モデルでは有効ではない。「確率分布の推定」の方が普遍的。

タグ：数楽

posted at 11:56:10

#数楽シュワルツの超函数論のような普通の数学に慣れている人なら、ひと目で「ベイズ推定法は収束しやすくなっているだろうな」と感じるはず。なぜならばベイズ推定法は事前分布という名のテスト函数φ(w)に対する∫f_n(w)φ(w)dw型の積分のn→∞での様子を扱うからです。続く

タグ：数楽

posted at 12:02:24

#数楽続き。それに対して最尤法ではナマのf_n(w)を扱います。f_n(w)が「暴れる」場合にはテスト函数で丸めて扱わないと苦しい。こういうことは普通に数学をやっていればみんな知っていること。ベイズ推定法の方が漸近論的には安全なことをやっているように見える。

タグ：数楽

posted at 12:05:49

『本の中身に言及してない』

え？Seki_yoさん、近藤誠氏の他の著書読んで『べつにおかしな点ない』って言ってるじゃないですか。反医療にご傾倒なんでしょ？あ、反ワクチンにも当然ご傾倒ですけどね。

twitter.com/seki_yo/status... pic.twitter.com/k6rjZopgdO

タグ：

posted at 12:07:25

#数楽 AICが使える易しい場合の話に戻る。正規分布、ガンマ分布、二項分布、…でそのまま書ける確率モデルは正則になります。リンク先ではガンマ分布で生成したサンプルから、ガンマ分布モデルと正規分布モデルで最尤推定して、AICを計算。
nbviewer.jupyter.org/gist/genkuroki...

タグ：数楽

posted at 12:13:45

#数楽ガンマ分布で生成したサンプルを正規分布モデルで推定する場合はAICを使ってよい場合から**外れて**います。そのような場合にどういう感じになっているかが
nbviewer.jupyter.org/gist/genkuroki...
を見ればわかります。

タグ：数楽

posted at 12:16:55

近藤誠の著書のおかげで、子宮頚癌(HPV)ワクチンにも脚光。Twitterで「HPVワクチン」で検索すると、ワクチン反対する人達の主張がわかります。「接種で死亡」とか「製薬会社の利権」とか、勧めている医師の誹謗中傷が列挙。データも産婦人科学会や厚労省が提示していないものばかりです

タグ：

posted at 12:19:22

#数楽 #JuliaLang 添付画像は

nbviewer.jupyter.org/gist/genkuroki...
AICと汎化損失の簡単な計算例

より。これは極めて簡単な話です。サンプルサイズ32。この場合にはガンマ分布モデルによるフィッティングの方がAICが小さく(尤度が大きく)なっています。 pic.twitter.com/NPTfOyPZe1

タグ： JuliaLang 数楽

posted at 12:24:27

#数楽正規分布から程遠いガンマ分布で生成したサンプルをガンマ分布モデルと正規分布モデルで推定してAIC(尤度)の大小でモデル選択すると、ほとんどの場合にガンマ分布モデルが選択されることになる。GLは数値積分で計算した汎化損失generalization lossです。 pic.twitter.com/WsA0cog8Hd

タグ：数楽

posted at 12:31:59

#数楽 #JuliaLang 正規分布にそこそこ近いガンマ分布でサンプルを生成した場合。この場合にはAIC(実質的に尤度)の大小でモデル選択すると、正規分布モデルの方が約16%の確率選択されています。 pic.twitter.com/HpUJz76AKB

タグ： JuliaLang 数楽

posted at 12:35:32

#数楽 #JuliaLang 正規分布に近いガンマ分布は正規分布に見えるサンプルを生成することが結構あります。 pic.twitter.com/Tpd6p6iEiU

タグ： JuliaLang 数楽

posted at 12:40:35

#数楽予測分布の相対精度の指標である汎化損失(GL, generalization loss)の推定値はサンプルだけからは計算できず、サンプルを生成した確率分布をカンニングしないと計算できません。AIC/(2n)はサンプルから簡単に計算できるGLの推定値になっています。

タグ：数楽

posted at 12:45:03

#数楽 GLとGLの可能な最小値の差はAICが使える上記では漸近的にカイ二乗分布に従います。以上のプロットを見ると、ガンマ分布モデルでの推定の方ではきちんとそうなっていることがわかります。

タグ：数楽

posted at 12:47:36

Haruhiko Okumura @h_okumura

話題の近藤誠氏の著書，うちの大学図書館にも11冊ある pic.twitter.com/PjkDenWTsf

タグ：

posted at 12:54:41

#数楽サンプルを生成したガンマ分布がそこそこ正規分布に近い場合にはサンプルサイズ32では16%程度の確率でガンマ分布より正規分布っぽく見えてしまっていたのですが、サイズ256ならその確率は0.22%まで下がりました。 pic.twitter.com/n2tOzgKfS1

タグ：数楽

posted at 13:07:50

#数楽確率密度函数 p(y) にサンプルY_1,…,Y_nを代入して得られる数値 p(Y_1)…p(Y_n) を尤度(likelihood)と呼びます。これがまた非常にわかりにくい概念だと思う。どうしてこれを「尤もらしさ」(もっともらしさ)と呼んでいいのか？続く

タグ：数楽

posted at 13:13:37

#数楽尤度 p(Y_1)…p(Y_n)は確率分布p(y)で測ったサンプルY_kが生じる確率の高さなのですが、尤度の意味での「もっともらしさ」はサンプルの側ではなく、確率分布p(y)の側のもっともらしさを意味していることになっています。どうしてそう考えてよいのか？

タグ：数楽

posted at 13:17:43

#数楽「〇〇をどうして××と呼ぶのか」という方向に忠実な疑問の持ち方は極めて有害。忠実になるのをやめて「〇〇は数学的にどのような性質を持つのか」という方向に疑問の持ち方を修正した方がよいです。そうした方が結果的に「どうして××と呼ぶのか」という疑問も解消することが多い。

タグ：数楽

posted at 13:22:51

内田樹さんてオレあんまり評価してなかったけど、この記事は一から十まで賛成だ。

"でも、これはまったく失敗だった。だって、怠け者の教員というのは評価しようとしまいと関係ないからです"

内田樹氏「日本の大学は滅びる」 #BLOGOS blogos.com/outline/256652/

タグ： BLOGOS

posted at 13:24:55

#数楽ヒトはしゃべることが大好きな動物なので、「どうしてそう呼ぶか」がどうしても気になる。そういう強いバイアスを持っていると思う。数学的なことを理解するために有害なバイアスがあることに注意しながら、疑問の持ち方を意識して修正するようにしないと苦しくなることが多い。

タグ：数楽

posted at 13:26:35

"評価システムを制度設計し、立ち上げ、維持運営するために、これまで研究教育で高い成果を上げて来た教員たちの時間と労力を奪うことになった
"評価システムの導入は、トータルでは、大学全体の研究教育のパフォーマンスを下げることにしかならなかった"

ちょうリアル。

タグ：

posted at 13:27:48

#数楽実はすでに示した数値計算の結果を見れば、どうして「尤度」=「もっともらしさ」=「likelihood」と呼んで良いのかに関する疑問は解消するはず。

数値計算結果へのリンク再掲：#JuliaLang
nbviewer.jupyter.org/gist/genkuroki...

タグ：数楽

posted at 13:30:12

メガネ21という企業が80年代から既に評価コストの莫大さというものを強く意識した経営をしてて、90年代には話題になってた。オレも読んで驚愕したものだったけど、役人っていまだに「そのコストはゼロである」って姿勢を崩さないんだよね。

タグ：

posted at 13:31:47

文藝春秋社は大手の出版社でステータスも高いと思うのだけれども、近藤誠の反ワクチン本を出すほど落ちぶれていたのかな。文藝春秋社はこの本の責任を取る気があるんですかね。これはやばいと文春の人に言わないと

タグ：

posted at 13:34:33

非公開

タグ：

posted at xx:xx:xx

#数楽正規分布に結構近いガンマ分布に従って生成された乱数列Y_1,…,Y_n(サンプルと呼ぶ)から、そのサンプルを生成した確率分布がガンマ分布と正規分布のどちらなのかを調べたい。ガンマ分布も正規分布もパラメーターを2個持っている。パラメーターは尤度を最大にするものを選ぼう。続く

タグ：数楽

posted at 13:35:44

#数楽続き。ガンマ分布と正規分布で最大尤度(ゆうど)が大きい方がもっともらしいと判断することにしよう。このとき、サンプルを生成した分布がガンマ分布であることを正解できる確率はどれくらいだろうか？その確率をモンテカルロシミュレーションで計算した結果をすでに紹介しました！！！

タグ：数楽

posted at 13:38:47

近藤誠氏に限らず、ワクチン否定、いわゆる反ワクチン情報を流すマスコミ関係者も同罪で、これは昔からよく使われる『ワクチン自閉症説』。タクラミックスさんが訂正されてるけど(twitter.com/takuramix/stat...)、医療ジャーナリストと称する人から訂正はなかったですね pic.twitter.com/tonK6pwI66

タグ：

posted at 13:39:21

文科省は「主観的な」評価ができないから、一見客観的っぽいクソみたいな軸で評価せざるを得ない、というのは現状認識の話として正しいと思う。文科省の責任回避としても正しいんだけど、これホント学生としてはたまったもんじゃない。

タグ：

posted at 13:39:31

#数楽サイズnのサンプルを分布Gamma(α=6.25, θ=0.8)で生成するとき、最大尤度の大小でガンマ分布と正規分布のどちらかを選択すると、

n=32 ⇒ 84%でガンマ分布だと正解
n=256 ⇒ 99.8%で正解

尤度はこういう数学的性質を持っている。

タグ：数楽

posted at 13:44:59

#数楽サンプルに対する確率分布の尤度の大小関係は、その確率分布がサンプルを生成した確率分布であるという予想の「もっともらしさ」の指標として使えることが以上の計算結果を見ればわかると思います。

こういうことは一応数学的に非自明です。非自明な数学的結果がすべてを支えているわけ。

タグ：数楽

posted at 13:48:55

#数楽続き。「〇〇に関する非自明な数学的結果」を認識できないと、結果的に「〇〇をどうして××と呼ぶか」に関する疑問は解消しないし、そもそもどう呼ぶかは非本質的であり、歴史的偶然で決まっているだけのことが多く、実用的に重要なのは非自明な数学的結果の方だけです。続く

タグ：数楽

posted at 14:00:17

#数楽続き。「数学的にどのように非自明なこと(素晴らしいこと)が起こっているか」についてきちんと説明してくれない教科書は個人的にはものすごく使い難い。学生に害をなす教科書を採用してしまう恐怖感が伴う。証明をきちんと書かなくても、説明するべきことは非常に多いと思う。

タグ：数楽

posted at 14:04:10

非公開

タグ：

posted at xx:xx:xx

#数楽「尤度」について「いぬどってなに？」のレベルでつまずくことの主な原因は、どのように非自明な(=素晴らしい)数学的結果が成立しているかをきちんと説明していないことだと思う。説明していればもっと高度なレベルで分からなくなっているはず。

タグ：数楽

posted at 14:13:47

#数楽「尤度」を未消化のまま「対数尤度」に出会って困惑した人は結構いると思う。

対数を考えるとたくさんの御利益があるのですが、特に「かけ算がたし算になる」という御利益のおかげで、大数の法則や中心極限定理を使えるようになります！！！

対数尤度も数学的非自明な結果と繋がる話。

タグ：数楽

posted at 14:18:59

#数楽確率分布q(y)に従う乱数の列Y_1,…,Y_n(サンプル)に関する確率分布p(x)の対数尤度の-1/n倍を

L_n = -(1/n)Σ_{k=1}^n log p(Y_k)

と書くと、大数の法則より、n→∞で

L_n → -∫ q(y) log p(y) dy.

タグ：数楽

posted at 14:23:32

#数楽続き。確率分布p(y)による確率分布q(y)のシミュレーションの精度はKullback-Leibler情報量

D(q||p) = -∫q(y) log p(y) dy - (-∫q(y) log q(y) dy)

であり、pに依存する第一項がL_nの収束先。続く

タグ：数楽

posted at 14:26:50

#数楽 p_1,p_2の予測精度の差

D(q||p_1)-D(q||p_2)=(-∫q(y)log p_1(y) dy)-(-∫q(y)log p_2(y) dy)

の右辺はp_1,p_2の対数尤度の-1/n倍の差の収束先になっています。続く

タグ：数楽

posted at 14:32:15

#数楽だから、予測精度を、サンプルから得られる情報だけから比較するためには、p_1,p_2の対数尤度を計算してそれらの大きさを比較すればよいわけです。ただし、これは大数の法則が有効になるほどnが大きい場合に限ります。続く

タグ：数楽

posted at 14:33:53

#数楽以上のように、対数尤度の概念を理解するためには、まず「大数の法則」が必須であり、その次に「Kullback-Leibler情報量が予測精度の指標になること」を意味する「Sanovの定理」も必須になっています。対数尤度の概念をすぐに理解できないのは仕方がありません。続く

タグ：数楽

posted at 14:35:07

#数楽「対数尤度すげえ！」と思ってもらえればうれしいです。しかし、驚きはこれで終わらない。

赤池情報量基準AICは「対数尤度よりすげえ！」ものです。対数尤度を知れば

(予測誤差) = - (1/n)(対数尤度) - (未知の定数) + o(1)

までたどりつける。続く

タグ：数楽

posted at 14:40:42

#数楽 AICについて知れば、AICを使える状況では

(予測誤差) = - (1/n)(対数尤度) + d/n - (未知の定数) + o(1/n)

とさらに精密なことが言えます。dは確率モデルのパラメーターの数です。(予測誤差はKL情報量のこと。)

タグ：数楽

posted at 14:43:42

#数楽サンプルサイズnに依存しない数に収束する項が -(1/n)(対数尤度) でそれによる近似の誤差は大体 d/n=(モデルのパラメーター数)/n になっているということです。誤差の大きさはdに比例し、nに反比例する。これがAICの大発見なのでした。

タグ：数楽

posted at 14:45:52

#数楽どうしてモデルのパラメーター数 d が出て来るかと言えば、思いっ切り省略すると、本質的なのは中心極限定理を使うことです。以上によって、

大数の法則
中心極限定理
KL情報量に関するSanovの定理

が3つとも出て来ました。これらは統計学で有用な確率論の基本定理です。

タグ：数楽

posted at 14:47:54

#数楽出て来た順に内容的に難しくなっていると思う。難易度は

大数の(弱)法則＜ KL情報量に関するSanovの定理＜中心極限定理

これらの解説は以下のリンク先にある。
genkuroki.github.io/documents/Intr...
genkuroki.github.io/documents/2016...

タグ：数楽

posted at 14:51:50

#数楽対数尤度の概念を理解するためには、最低でも、大数の法則とKullback-Leibler情報量に関するSanovの定理の理解が必須だと思います。大数の法則についてはほぼすべての教科書で解説されていますが、Sanovの定理の良い解説は見つけ難いです。だから、自分で書いた。

タグ：数楽

posted at 14:53:12

#数楽あと、中心極限定理の証明も、モーメント母函数や特性函数を使った本質的にLaplace-Fourier解析を使う議論ではなく、大学1年生レベルのテイラーの定理だけを使った簡単な証明があることについても教科書で触れておくべきだと思いました。だから、自分で書いた。

タグ：数楽

posted at 14:54:23

でえもん @GreatDemon1701

@rikomrnk @genkuroki 黒い奴ほどよくゴネる。

タグ：

posted at 14:59:52

#数楽まとめ1：未知の確率分布q(y)が生成したサンプルY_1,…,Y_nだけから、確率分布p(y)の未知の分布q(y)の予測誤差の大小関係は、nを十分に大きくすれば、対数尤度の-1/n倍-(1/n)Σ_{k=1}^n log p(Y_k) の大きさで比較できる。

タグ：数楽

posted at 15:00:22

#数楽まとめ2：できれば、nをあまり大きくせずに何とかしたい。そのためにはより精密な数学的結果が必要である。そのような精密な結果の代表格が最尤法における赤池情報量基準AICである。現在ではベイズ推定法のWAICに一般化されている。

タグ：数楽

posted at 15:02:15

#数楽まとめ3：対数尤度の概念(これはとても基本的)を理解するためには、大数の法則とKullback-Leibler情報量に関するSanovの定理が必須である。統計学で有用な確率論における3つの定理の難易度の順番は

大数の弱法則＜ Sanovの定理＜中心極限定理

タグ：数楽

posted at 15:04:37

#数楽 #JuliaLang おまけ：関連の数値計算を気軽にかつ高速に行うには、Julia言語とJupyter notebookは極めて有用である。実際に有用であることの証拠は以下↓

nbviewer.jupyter.org/gist/genkuroki...
nbviewer.jupyter.org/gist/genkuroki...

タグ： JuliaLang 数楽

posted at 15:08:39

#JuliaLang Julia言語とJupyter notebookの組み合わせを最も簡単に利用する手段は

next.juliabox.com

を利用することです。Googleのアカウントを持っていればすぐに使い始められます。

タグ： JuliaLang

posted at 15:09:53

#JuliaLang 自分のパソコンでJulia言語＋Jupyter notebookを利用したければ

nbviewer.jupyter.org/gist/genkuroki...
WindowsへのJuliaのインストール

を見て下さい。Anaconda+Julia言語の組み合わせが楽です。

タグ： JuliaLang

posted at 15:12:22

#JuliaLang 「サンプルを1万個生成して、その各々について、汎化損失を数値積分で計算して、AICと比較する」のような計算を

nbviewer.jupyter.org/gist/genkuroki...

でやっているのですが、単純な繰り返しや数値積分の計算などが遅いと相当に面倒なことになります。

タグ： JuliaLang

posted at 15:14:35

#JuliaLang 私が公開しているJulia言語のJupyter notebookではほぼ常に時間がかかりそうな計算をする場所には{at}timeマクロを挿入してあって、私のパソコンでかかった時間も全部公開されていたりします。こういう習慣は広まって欲しいと思う。

タグ： JuliaLang

posted at 15:16:08

#JuliaLang 「高性能パソコンで数十時間連続して計算して得た結果です」とか言われると、自分では試す気が失せる人が多いと思うのですが、「数秒で計算が終わります」とか「長くても数分で計算が終わります」ということがわかっていれば再検証してくれる人も出て来易いと思う。

タグ： JuliaLang

posted at 15:17:43

砂___の___女 @vecchio_ciao

@AS_Insects そうです、そうです。
“先生の言うことは絶対。なぜなら、先生だから。”という以外の根拠が何もなく、それ以来、何を言ってもアレな感じだな〜としか思えませんね。

タグ：

posted at 15:31:27

非公開

タグ：

posted at xx:xx:xx

砂___の___女 @vecchio_ciao

@AS_Insects 同感です。
いわゆる「良さげ」なのが回ってきても、言葉の端々に“俺偉い”“してやってる”“理解してやってる”態度が見え見えでうんざりしてました。
実際、学校でもよく遭遇するタイプですけど😅

タグ：

posted at 15:42:16

⚡️ "AICとか対数尤度とかについて"

twitter.com/i/moments/9277...

タグ：

posted at 16:13:12

.@vecchio_ciao さんのコメント「この人は #掛算の件でもアレなことを言っていた人。」にいいね！しました。 togetter.com/li/1169029#c43...

タグ：掛算

posted at 16:28:20

#数楽補足：サンプルY_1,…,Y_nに関する確率分布(密度函数)p(y)の尤度の定義は p(Y_1)…p(Y_n) で、対数尤度はそのlogである

log p(Y_1) + … + log p(Y_n).

和になっているのでnで割って平均の形にして、大数の法則を使える。

タグ：数楽

posted at 18:02:08

#数楽サンプルY_1,…,Y_nが確率分布q(y)で生成されているとき、大数の法則より、(f(Y_1)+…+f(Y_n))/nはn→∞でf(y)のq(y)に関する平均 ∫q(y)f(y)dyに収束する。だから(対数尤度)/nはn→∞で∫q(y)log p(y) dyに収束する。

タグ：数楽

posted at 18:05:09

#数楽 (対数尤度)/n は ∫q(y) log p(y) dy の推定量になっている。それで何がうれしいのかを理解するためには、Kullback-Leibler情報量に関するSanovの定理を知っていることが必須。続く

タグ：数楽

posted at 18:06:50

#数楽 KL情報量の定義：

D(q||p) = ∫q(y)log(q(y)/p(y))dy.

Sanovの定理：確率分布p(y)で長さnの乱数列を発生させたとき、その乱数列が確率分布q(y)の乱数列でないことがばれずに済む確率の対数はほぼ -n D(q||p) になる。

タグ：数楽

posted at 18:15:10

#数楽すなわち、ばれずに済む確率は exp(-n D(q||p) + o(n)) と振る舞う。

これはKullback-Leibler情報量 D(q||p) がpによるqのシミュレーションで「ボロが出る速さ」になっていることを意味する。

タグ：数楽

posted at 18:17:34

しーちゃん @SHIii_sama

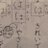
小2の算数で習う「計算の工夫」っていう単元が控え目にいっても糞。
50ー6を求めるのにこんなに分解しないとだめ？
この単元のときに親族の結婚式で欠席だったのは幸いか。
「どう工夫したかを書け」という出題者の意図がわからずテストで軒並みマイナスされてたけど、まあいい。
#超算数 pic.twitter.com/KZfYWsiVaf

タグ：超算数

posted at 18:18:56

#数楽最も簡単なKL情報量の話。これから毎日ずっと(確率q=1で)雨が続くと仮定する。天気予報士は確率pで雨の目が出るサイコロを振って予報を発表すると仮定する。このとき、n日間のあいだ予報が当たり続ける確率はp^nなのでその対数は n log p になります。続く

タグ：数楽

posted at 18:19:21

#数楽 n log p = -n(-log p)でかつ、q=1のとき、KL情報量は

D(q||p) = q log(q/p) + (1-q)log((1-q)/(1-p)) = - log p.

n日間確率pで予報が当たり続ける確率の対数は -n D(q||p) に等しい。

タグ：数楽

posted at 18:21:13

残り30件のツイートを見る

#数楽続き。KL情報量に関するSanovの定理は以上の自明な場合の話の非自明な一般化になっています。D(q||p)は確率分布pによる確率分布qのシミュレーションでボロが出る速さなので、それが小さいほどそのシミュレーションの精度は高いということになります。続く

タグ：数楽

posted at 18:22:55

#数楽続き。未知の確率分布q(y)を予測するために作られた確率分布p(y)の精度はKL情報量 D(q||p) を計算できればわかります。しかし、qが未知なので D(q||p) を直接計算することは不可能です。確率分布qが生成したサンプルだけを使って何とかする必要がある。続く

タグ：数楽

posted at 18:24:21

#数楽続き。出発点になるのが、「対数尤度」という素晴らしいアイデア。対数尤度の-1/n倍

L_n = - (log p(Y_1)+…+log p(Y_n))/n

は大数の法則より、n→∞で

G(q||p) = -∫ q(y) log p(y) dy

に収束します。続く

タグ：数楽

posted at 18:26:55

ほうら、近藤誠氏叩きに危機感を覚えた、反ワクチン沸いてきたよ～。印象論をいつも拡散している方々に言われたくないね～。学会や厚労省、まともな論文で医学的反論をされたらいかが？とんちんかんさん

twitter.com/ahare_asayaka/...

タグ：

posted at 18:29:37

#数楽続き。そして、KL情報量は

D(q||p) = G(q||p) - I(q), I(q)=G(q||q)

と書き直せます。だから、

D(q||p_1) - D(q||p_2) = G(q||p_1) - G(q||p_2).

続く

タグ：数楽

posted at 18:32:33

#数楽もしも、L_n で G(q||p) を十分な精度で近似できるほどサンプルサイズnを大きくできるならば(可能な場合も現実には厳しい場合もある)、p_1とp_2のL_nの大きさを比較して、p_1とp_2のどちらの予測精度が高いかを判定できる。これが対数尤度の基本的なアイデア。

タグ：数楽

posted at 18:34:06

#数楽 nをあまり大きくできない場合には、汎化損失G(q||p)のL_nによる近似の誤差の主要項が何であるかがわかると、あまり大きくないnで予測分布の精度を比較できるようになります。最尤法の場合にはAICが使え、ベイズ推定法ではWAICが使える。

タグ：数楽

posted at 18:36:23

その前に、なぜワクチンが不要なのか、医学的根拠を示して反論してくださいよ、とんちんかんな回答せずにね。

twitter.com/ahare_asayaka/...

タグ：

posted at 18:55:56

研究に集中してくれればそれで十分なんですよ。書類なんか書かないでいい。「社会人として合格」な人は足し算でしか利かない仕事をしてるようなもんで、今後は全部AIに代替されます。必要なのは掛け算で利いてくる新分野。これには大量の研究者がピラミッドの底辺のように必要なんです。 twitter.com/manavee_milk/s...

タグ：

posted at 19:38:03

Chihiro M. @chivillain

辛くもあり、生半可な覚悟ではいかないけれど、育児は基本的に人生で指折りの喜びだと想像している。この喜びを経験するのにきっと性別は全く関係ない。 goo.gl/gbmQnk pic.twitter.com/qUJGv9fPP9

タグ：

posted at 20:00:30

松浦晋也 @ShinyaMatsuura

S (ﾂｲｰﾄはｽﾚｯﾄﾞ全体をご確認く @esumii

どう考えてもくだらん書類作成をこなすことを、社会人として機能している証明と考える人がいるんだな↓RT あんなもん、やらんですむならやらんに越したことはない。「いやなことでもやるのが社会人の証明」ではないよ。「いやなことをしないですむ社会を作る」のが社会人の責務。

タグ：

posted at 20:41:42

@ksknac @camloeba あれ、まさにcallccの型が（例えばHaskellでもモナドを無視:-)すれば）((a -> b) -> a) -> aなんですが、そういう話ではなく？

タグ：

posted at 20:59:09

非公開

タグ：

posted at xx:xx:xx

Juliaにおける最適化モデリングライブラリJuMP入門 - MyEnigma myenigma.hatenablog.com/entry/2017/07/...

タグ：

posted at 21:10:37

前野［いろもの物理学者］昌弘 @irobutsu

Pythonの画像描画ライブラリ「Matplotlib」の、機械学習で使われる典型的なグラフ機能：Pythonで始める機械学習入門（5） - ＠IT www.atmarkit.co.jp/ait/articles/1...

タグ：

posted at 21:11:25

非公開

タグ：

posted at xx:xx:xx

出世払いは「無償化」じゃないし、年収２５０万は「出世払い」が始まるほどの出世じゃない。
「無償化」とか「出世払い」とか呼ぶのは恥ずかしいので、潔く「借金」と呼べ。

自民党：大学授業料、「出世払い方式」検討を - 毎日新聞 mainichi.jp/articles/20171...

タグ：

posted at 21:24:01

Juliaで学ぶ画像処理〜ニューラルネットワーク(Neural Network) part1〜 - IMACEL Academy -人工知能・画像解析の技術応用に向けて-|LPixel(エルピクセル) lp-tech.net/articles/SEFVJ

タグ：

posted at 21:27:32

Four Options for Full Text » Health Science Center Libraries » UF Academic Health Center » University of Florida library.health.ufl.edu/2017/08/16/fou...

タグ：

posted at 21:29:44

ワクチンで自閉症デマも相変わらず散見。「情報隠ぺい」とか「国家の陰謀」とか、反ワクチンの人達は都市伝説好きね。

ワクチンほど発売前後で情報開示し、安全性検証してる薬剤はないけどね。「治療」する薬は効果が見えやすいけど、「予防」する薬は効果が見えにくいから叩かれやすいのだろうけど

タグ：

posted at 21:56:21