黒木玄 Gen Kuroki(@genkuroki)/2019年08月/Page 28

#つぶやきProcessing
f=0
draw=_=>{createCanvas(w=640,w)
t=translate
s=scale
t(0,w/2)
for(j=f--;j<f+280;j++)if(j%20==0){
push()
s(pow(1.15,(j-f)/9))
t(m=15,m)
g(7)
pop()}}
g=(c)=>{if(c){line(0,0,0,d=-9)
t(0,d)
for(i of[-.3,.3]){push()
rotate(i)
s(.2+noise(j*i+m++))
g(c-1)
pop()}}} pic.twitter.com/OmHoXbqxah

タグ：つぶやきProcessing

posted at 00:00:58

#超算数　「普通に考えると」とあるけど、筆者や日本の算数教育界の考えが普通ではなく非常識だから pic.twitter.com/wDCIcxHpbJ

タグ：超算数

posted at 00:03:52

#超算数　次は除法。この流れから予想されるように、筆者は除法には等分除と包含除の２つの意味があるという立場。

　そういう誤った認識で、外国の割り算指導を見るから、当然おかしなことになってしまう。

タグ：超算数

posted at 00:07:48

#超算数　子供たちはおかしな算数教育にもかかわらず、

等分除と包含除も区別しないという正しい認識になっている。

筆者はこれを「混乱」というが、混乱しているのは筆者（と、算数教育界の専門家）である。 pic.twitter.com/L0tPP3V3n2

タグ：超算数

posted at 00:13:55

#超算数　ベトナムの除法についてこんな感じ。

「掛け算の順序や等分除と包含除に拘る日本の算数指導がおかしいのでは？」とか思わないのかな？ pic.twitter.com/LwHPJH0o1q

タグ：超算数

posted at 00:18:13

#超算数　インドネシアの割り算指導をdisりまくり

p138　【ここに同国の除法の導入学習における大きな躓きがあるが】

p139　【誤った累減についての理解】 pic.twitter.com/KwCinfrQh4

タグ：超算数

posted at 00:43:31

#超算数
p141　【明らかに論理的な間違い】

p142　【誤解を生む練習問題】

p142　【教科書編集者の知識不足】【真摯に反省すべき】

筆者自身のおかしな認識こそ反省すべき pic.twitter.com/8RiKPoVM5E

タグ：超算数

posted at 00:48:07

#超算数

「児童の理解を混乱させる」と言っているが、具体的にどういう混乱なのか？

「割り算には等分除と包含除がある」という筆者の認識こそが大きな混乱であることに気がつかないのか？ pic.twitter.com/8tBclAZaWe

タグ：超算数

posted at 00:58:39

勝川俊雄 @katukawa

このサイトはいろんな国の経済データのグラフを作れて面白い。
www.ceicdata.com/datapage/en/se...

タグ：

posted at 01:00:48

ファインマンbot @feynmannnn

大きな結晶を含むようなスズの細い針金をとり、耳の近くに保持しながら引っ張ると各結晶の面が突然ずれていくのがよくわかる。面がつぎつぎに新しい位置へ飛ぶときの「カチッ」という音をきくことができる。

タグ：

posted at 01:01:24

#超算数　ネパールの割り算指導

【「等分除」はない!?】というタイトルになっているけど、

45個の林檎を7人で分けると1人何個？

というのもちゃんと扱っている。

にもかかわらずこのようなタイトルにしてしまう。これも筆者の混乱を示している。 pic.twitter.com/QtM2rZ4WO3

タグ：超算数

posted at 01:14:22

#超算数　なぜ図が人ではなく箱だと、等分除ではなく包含除としている証拠なのか、私にはさっぱり分からない。 pic.twitter.com/G6Gupi3Wh7

タグ：超算数

posted at 01:21:13

#超算数　筆者は「累減は包含除であって、等分除ではない」と思い込んでいるから、こうやって難癖を付けることになるが、この筆者の思い込みこそが大きな誤りである。 pic.twitter.com/WxsA9ecups

タグ：超算数

posted at 01:27:38

#超算数

12個の蜜柑を4人に分けるときに、各自に1個ずつ配ると4個減る。と言う具合に考えれば

12-4-4-4＝0で3回4を引けば0になるから、1人4個

こうすれば、包含除どうよう累減と考えられ、結局等分除、包含除の区別に意味がないことになる。

これは、遠山啓も言っていることである。

タグ：超算数

posted at 01:29:38

#超算数　ただし遠山啓は「分離量では等分除と包含除の区別はないが、連続量だと区別がある」というような間違ったことも言っているから、要注意。

タグ：超算数

posted at 01:30:27

#超算数　この後も分数や小数などいろいろあるが、疲れたのでこの辺にしておく。

　筆者紹介と参考文献を貼り付けておく。知っている名前がちらほら出てくる。 pic.twitter.com/GN1FSDzMzp

タグ：超算数

posted at 01:35:35

#超算数 pic.twitter.com/YcX4lE4aNA

タグ：超算数

posted at 01:45:58

#超算数　ここに紹介されている
　
わっさき「わり算、等分除、包含除、トランプ配り」2013年
takehikom.hateblo.jp/entry/2030605/...

は見つけられなかった。 pic.twitter.com/8MXjWMECTc

タグ：超算数

posted at 01:51:20

Hacker News @HNTweets

ごまふあざらし(GomahuAzaras @MathSorcerer

A book from Alan Turing and a mysterious piece of paper: blog.stephenwolfram.com/2019/08/a-book... Comments: news.ycombinator.com/item?id=20812294

タグ：

posted at 02:50:02

Gomah.jl
max pooling の padding の差で誤差があった現象を回避したできゅ．

タグ：

posted at 03:08:32

非公開

タグ：

posted at xx:xx:xx

@sekibunnteisuu #超算数 URLが違うからですね。正しくはtakehikom.hateblo.jp/entry/20130605...。それにしてもわさっき見ているなら、このタグも読んでいるかもしれません。

タグ：超算数

posted at 07:02:49

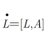
Integrable Systems, @integrablesys

Did you know that a well-known Japanese mathematician Shizuo Kakutani was born in 1911 #OnThisDay? To celebrate, read for free a survey on Kakutani-type fixed point theorems at rdcu.be/bPGir @adhara_mathphys @genkuroki @hayano
Link made using HT➡️twitter.com/OpenScienceR/s... pic.twitter.com/8Yol0cCgTw

タグ： OnThisDay

posted at 07:19:09

Nyoho @NeXTSTEP2OSX

昨日は昼間に #TeX を頑張って \expandafter を完全に理解しました。\noexpandも必要に応じて使えるようになりました。

タグ： TeX

posted at 08:16:28

#統計【「どういう分布だと想定するのか」】

任意の分布。

まずは{1,0}上の任意の確率分布を2つ考えて、KL情報量をプロットしてみたら？

確率分布Q：1の確率q, 0の確率1-q
確率分布P：1の確率p, 0の確率1-p

KL(Q,P) = q log(q/p) + (1-q)log((1-q)/(1-p))

下に凸な函数

twitter.com/tsatie/status/... pic.twitter.com/zsfRZZ0UMI

タグ：統計

posted at 10:37:12

#統計あと、a,bを正の整数としてq=b/aとおいて、二項分布での確率

P(n,k) = binom(n, k) pⁿ(1-n)ⁿ⁻ᵏ

で n = Na, k = Nb (そのとき k/n=q) とおいて、対数を取って-1/nをかけたもの

(-1/Na) log P(Na, Nb)

のN→∞での極限を計算してみるとか。区分求積法で行ける。大学入試問題レベル。

タグ：統計

posted at 10:46:19

#統計答えはKL情報量になる。

n,pに対する二項分布におけるk/n=qとなる確率の対数の-1/n倍の極限は

q log(q/p) + (1-q)log((1-q)/(1-p))

になる。大雑把にはこれの-1倍は「nが大きなときの、pの二項分布で偶然に確率がqであるかのように見える場合の確率の対数の1/n倍の近似値」です。

タグ：統計

posted at 10:52:13

#統計一段難しい問題：0<p<1, 0<q₀<q₁<1 のとき、二項分布における

(-1/n)log Σ_{q₀ ≦ k/n ≦ q₁} binom(n,k) pⁿ(1-p)ⁿ⁻ᵏ

のn→∞での極限を求めよ。和は q₀ ≦ k/n ≦ q₁ を満たすkについて取る。

この問題は大偏差原理の非自明な最も簡単な例になっていると言ってよいと思う。

タグ：統計

posted at 10:58:36

#統計以上において、binom(n,k) = n!/(k!(n-k)!), 二項係数。

タグ：統計

posted at 10:59:40

#統計 KL情報量についてやっておくべき練習問題には

q(x)がℝ上の任意の確率密度函数で平均μ₀と分散σ₀²を持つものだとし、p(x)=exp(-(x-μ)²/(2σ²))/√(2πσ²), 正規分布の確率密度函数としたときの

KL(q,p) = ∫_ℝ q(x) log(q(x)/p(x)) dx

をμ₀,σ₀,μ,σ, S(q)=-∫q(x) log q(x) dxで表す計算。

タグ：統計

posted at 11:18:59

#統計そして、q(x)が固定されているとき、KL(q,p)を最小にするμ,σをμ₀,σ₀で表す計算。(記号的に答えがばればれ！😊)

タグ：統計

posted at 11:19:01

#統計以上は与えられた任意の確率分布qをもっともよくシミュレートする正規分布pを求める計算そのものになっている。

この計算によって未知のqの平均と分散の推定は本質的に正規分布モデルpによる推定になっていることもわかる。

KL情報量を通して「何をやっているか」がより明確になる。

タグ：統計

posted at 11:19:01

#統計私は20世紀の統計学史に詳しくないのですが、以上のようにKL情報量の視点から統計学の諸概念を整理することによって、それまでにはよくわかっていなかったことをクリアに理解できるようにしたのは赤池弘次さんだと思っています。

統計学入門の解説をする人は赤池さんをもっと絶賛するべき。

タグ：統計

posted at 11:19:02

#統計 1980年の赤池弘次さんの2つの論説

ismrepo.ism.ac.jp/?action=pages_...
統計的推論のパラダイムの変遷について
赤池弘次
1980

www.jstage.jst.go.jp/article/butsur...
エントロピーとモデルの尤度
赤池弘次
1980

赤池さんによればFisherさんは尤度(ゆうど)について十分に理解していなかった。

タグ：統計

posted at 11:19:02

#統計 KL情報量はもっと一般的なdivergenceに一般化されるのですが、赤池さんはそういう一般化された方向からKL情報量(=相対エントロピーの-1倍)にたどり着いたのでは__ない__。

論説を見れば分かるように、KL情報量が大偏差原理の特殊な場合に自然に出て来てしまうことを基礎にしています。

タグ：統計

posted at 11:23:11

#統計非常に残念なことに、ググると一般化されたdivergenceに関する解説の方が、「KL情報量が確率論的に自然に出て来てしまうという事実」(Sanovの定理)の解説より見つけ易い感じになっていると思います。易しい場合について書いた私による解説が

genkuroki.github.io/documents/2016...

にあります。

タグ：統計

posted at 11:31:30

フルーツキッチンほのか @FK_honoka

#統計易しい解説への分岐

twitter.com/genkuroki/stat...

タグ：統計

posted at 11:34:24

ブドウは房のままだと
カビが生えます。

このように枝ごと切り平たく
風通しの良い涼しい場所で保管すると１週間以上も長持ちします。

枝をちぎり実だけにしてしまうと甘味が抜けてしまうのでご注意を。

農家さん直伝の知恵です。
ぶどう好きに広まれっ
#歩乃果術 pic.twitter.com/Y6JkZRftlY

タグ：歩乃果術

posted at 12:10:19

今野滋 @konno3

@genkuroki ありがとうございます！
juliamath.github.io/FFTW.jl/latest...
の説明を見て関数 r2r の使い方がわからずスタックしてました
普通に関数 fft() があったとは..
人に聞かなければわからなかったです pic.twitter.com/dM58Svojyu

タグ：

posted at 12:50:28

#統計問題追加：以下のリンク先の練習問題におけるp(x)がLaplace分布の確率密度函数

p(x) = (1/(2b)) exp(-|x-a|/b)

の場合について考えてみよ。

ヒント：q(x)について

a₀ = (q(x)の中央値),
b₀ = (|x-a₀|のq(x)での平均) = ∫_ℝ |x-a₀| q(x) dx

とおけ。

twitter.com/genkuroki/stat...

タグ：統計

posted at 12:56:37

#統計要するにKL情報量の視点から見ると、中央値と|x-(中央値)|の平均に特に注目することは、本質的にLaplace分布モデルによる推定をやっていることになります。

まとめ：

平均と分散の推定 ⇔ 正規分布モデルによる推定

中央値と|x-(中央値)|の平均の推定 ⇔ Laplace分布モデルによる推定

タグ：統計

posted at 12:56:39

#統計さらに面倒な問題：最頻値についてはどうか？

まあ、とにかくも、KL情報量について理解すれば真に易しい統計学入門に出て来る諸概念を「未知の確率分布の確率分布モデルによる推定(推測)」というアイデアで整理できたりするわけです。

タグ：統計

posted at 12:56:40

@temmusu_n 思いっきり間違えていましたね^^

タグ：

posted at 12:57:41

#超算数黒木さんが言及している遠山啓氏は、戦後算数教育を文部省や検定教科書の枠外から牽引した有名人。全体として文部省や算数教育界主流派に反対の立場であっても、#掛算の順序を否定できないことでは主流派と一致していました。戦後算数教育の主流派の面々の掛順固定ぶりを概観しましょう。 twitter.com/genkuroki/stat...

タグ：掛算超算数

posted at 13:21:26

#超算数まずは塩野直道氏。この人は戦前の国定算術教科書を編纂したのですが、戦後は公職追放に逢い、追放解除後も官には戻りませんでした。塩野の戦後の主な活動は啓林館という教科書会社での教科書出版でした。1955年の第2回目の算数教科書出版で、4×5と5×4は違うと指導twitter.com/metameta007/st...。

タグ：超算数

posted at 13:21:27

#統計「さらに面倒な問題：最頻値についてはどうか？」のヒント

q(x)の最頻値 = q(x)を最大にするxの値

δ(x-a)のq(x)に関する平均 = q(a)

なので

p(x|a) = const. exp(-(δ(x-a)を近似する非負値函数の定数倍))

で定義される確率モデルp(x|a)でaを推定すると最頻値の近似的な推定になる。

タグ：統計

posted at 13:29:33

#統計最頻値に関する話はすっきりしないが、確率分布モデルの確率密度函数の形が単峰型になっていることに注目。

推定対象の母集団分布が単峰型になってなさそうなことが明らかになってしまったなら、平均、中央値、最頻値に特に注目する意義は薄くなったと考えるべきだと思われます。

タグ：統計

posted at 13:34:36

#超算数次に和田義信氏。文部省の算数担当者としては塩野から2代後の人です(間に前田隆一、森規矩男のコンビがいるが割愛)。この人は最初の1947年学習指導要領から1958年版まで関与した戦後算数教育の超大立者です。おそらく51年指導要領に関連して掛順固定の廃止を提案twitter.com/OokuboTact/sta...。

タグ：超算数

posted at 13:35:24

#統計多分、以上のようなKL情報量を用いて「未知の確率分布の確率分布モデルによる推定・推測」という考え方で全てを整理することは、統計学入門を教える側が理解を深めるために大いに役に立つものと思われます。

統計学入門を教わる側がいきなりKL情報量のような話を理解するのは多分結構大変。

タグ：統計

posted at 13:38:29

#統計赤池さんが強調しているように、統計学における最も基本的な概念である尤度(ゆうど)について理解するにもKL情報量のSanovの定理が必須。

平均、中央値、最頻値、分散、…について確率分布の視点から理解するためにも、KL情報量の理解が必須。

などなど

タグ：統計

posted at 13:41:08

#統計個人的な感覚では「情報量統計学」のように表現することが適切な話をしているつもりはない。

理解のためには「KL情報量」という用語に「情報量」という用語が入っていることを無視しても問題ない(むしろ無視するべき)ことを上で強調した。

大偏差原理の特殊な場合であるSanovの定理が重要。

タグ：統計

posted at 13:47:16

#統計母集団からの無作為抽出の統計学における確率論の三種の神器は

* 大数の法則
* 中心極限定理
* Sanovの定理

中心極限定理によって正規分布が自然に出て来るのと同じような感じで、Sanovの定理によってKullback-Leibler情報量(と呼ばれているもの、情報量だと思う必要はない)が自然に出て来る。

タグ：統計

posted at 13:51:49

#超算数上は読みようによっては、和田は都教育庁の根本力雄氏と石田貞一氏に掛順廃止の提案を妨げてられたか翻意させられたようにも見える。しかし1954年に和田が著した「式とその指導」という自信作を読むと、和田の掛順反対は不徹底だったことが分かった。

タグ：超算数

posted at 13:53:36

#超算数私は、54年に中教出版から出たパンフレットは入手できず、1997年に出た和田の著作集第2巻に採録された版を参照しました。その103ページで和田は、速さの文章題でさえ「トランプ配り」論法が妥当することを述べ【上の問題でいえば、4×5と式を書くだけではなくて、時に5×4とする者があっても→

タグ：超算数

posted at 13:54:06

#統計正規分布もKL情報量も、「天下り的に定義が与えられたもの」のように見えていると苦しくて、「勝手に自然に出て来てしまう数学的対象なので、避けて通れないもの」のように見えないと苦しい。

それらをどのように呼ぼうが勝手に出て来るので扱わざるを得ない。呼び名はどうでもよい。

タグ：統計

posted at 13:55:56

#超算数、これがどうして意味づけられるかを指導して、その意味を明らかにする機会、ここで突込んだ割合についての考えを指導する機会をつかむようにしたいと考えるのである。】と言っています。要するに逆順の #掛算の式は、子供がトランプ配りの考え方で説明できて初めて許可できるという方針。

タグ：掛算超算数

posted at 13:57:56

Gabriel Peyré @gabrielpeyre

Oldies but goldies: A. Legendre, Nouvelles méthodes pour la détermination des orbites des comètes, 1805. First publication of the least square method, before Gauss according to French people … projecteuclid.org/download/pdf_1... pic.twitter.com/IdzfTsR5AV

タグ：

posted at 14:00:00

#統計数学的補足：有限集合上の確率測度ではなく、もっと一般の場合のSanovの定理の証明を知りたい人は、Varadhanさんの講義録

math.nyu.edu/~varadhan/LDP/...

などを参照。そこでは本質的に、無限次元のCramerの定理を経由して、自由エネルギーのLegendre変換でKL情報量が出て来ることを示している。

タグ：統計

posted at 14:02:06

#超算数同様の方針は、1980年の文部省による算数指導書twitter.com/temmusu_n/stat...にも見られる。和田の方針が文部省に採用され長く残ったと考えてよいと思います。因みに、和田は1996年まで在世し、叙勲もしています。

タグ：超算数

posted at 14:06:23

#統計「自由エネルギー」と「エントロピー」(KL情報量の-1倍は相対エントロピー)の統計力学における関係を知っていれば、その手の話をi.i.d.というトイモデルで実行していると思ってもよいです。

タグ：統計

posted at 14:07:13

#超算数中島健三氏は、和田の次に文部省で算数を担当。和田も58年指導要領に関与したが、すでに官を離れていた。文部省で編集を主導したのは中島。同指導要領は乗法の記号を【正しく用いること】を謳い、59年に出た半公式解説本の中島担当箇所はこれを掛順固定であると説明mobile.twitter.com/temmusu_n/stat...。

タグ：超算数

posted at 14:11:59

#統計もとの易しい話に戻る。

統計学や機械学習では「損失函数の期待値を最小にしたい」というようなことが述べられます。

以下のリンク先の話は「損失函数の期待値」と「p(x)=const.exp(-(損失函数))型の確率分布モデルによる推定」の関係の初歩的な例になっています。

twitter.com/genkuroki/stat...

タグ：統計

posted at 14:15:50

#統計リンク先に追加

* 「損失函数の期待値の最小化」と「未知の確率分布のconst. exp(-(損失函数))型の確率分布モデルによる推定」の同値性を理解するためにもKL情報量に関するSanovの定理の理解が必要。

こんな感じで基本的で大事なことが芋蔓式に出て来る。

twitter.com/genkuroki/stat...

タグ：統計

posted at 14:19:42

#統計多分、以上に話は、「平均、中央値、最頻値云々」のような統計学入門に十分に触れる前に、渡辺澄夫『ベイズ統計の理論と方法』のような「未知の確率分布の確率分布モデルによる推定」系の本を読んでしまった人が、統計学入門をどう理解すればお得であるかの解説にもなっていると思う。

タグ：統計

posted at 14:25:10

Haruka Ozaki (尾崎遼) @yuifu

コードの実行し忘れに気づくという意味で、RStudioよりJupyterの方が便利な気がしてきた

タグ：

posted at 14:32:34

#超算数　
　
わっさき「わり算、等分除、包含除、トランプ配り」2013年

ありました。

takehikom.hateblo.jp/entry/20130605...

タグ：超算数

posted at 14:56:05

#超算数　日本のおかしな算数教育界の教義に嵌まってしまって、外国の算数指導が歪んで見える例は他にもある。

算数授業研究ＶＯＬ．８０（２０１２年）算数授業論究論究２かけ算を究める
honto.jp/netstore/pd-bo...

から

タグ：超算数

posted at 14:58:49

【我々は、何を、なぜ、いかにして教えるか
筑波大学教育開発国際協力研究センター　磯田　正美】 pic.twitter.com/RcdYtYIYWv

タグ：

posted at 15:01:08

#超算数
要するに、

「日本では、3を4個足すのが3×4で、九九も、3×2、3×3、3×4、となっている。

中国では、3を4個足すのは4×3で、それに応じて九九も日本とは逆に、2×3、3×3、4×3、になっている。

ところがスペインは、中国同様3を4個足すのは4×3なのに、九九は日本と同じだからおかしい」

タグ：超算数

posted at 15:07:05

#超算数　と言いたいらしいが、おかしいのは磯田正美の考えであり、日本の算数教育界の考えである。

必要を認めない教師、子どもが生まれることの何が問題なのか？

おかしなイデオロギーに浸かっていると、自分の側が歪んでいることに気づかなくて他者が歪んで見えてしまうようだ。 pic.twitter.com/5YloU8muFW

タグ：超算数

posted at 15:12:00

#超算数　
【小学校でかけ算を教えるのは何のためか　ディポール大学教育学部　高橋　昭彦】

「かけ算に関しても、日本では想像もつかないような指導がまかり通っている」は間違い

正しくは

かけ算に関しても、日本の小学校では、世間一般の常識からは想像もつかないような指導がまかり通っている pic.twitter.com/xGAXicbkpo

タグ：超算数

posted at 15:23:03

#統計

正規分布 const. exp(-(x-μ)²/(2σ²))

と

Laplace分布 const. exp(-|x-a|/b)

では x→±∞ での後者の減少速度の方が圧倒的に遅い。Laplace分布のサンプルの方が外れ値に見える値を相対的に含み易くなります。Laplace分布による推定値の中央値も外れ値に強い。

twitter.com/genkuroki/stat...

タグ：統計

posted at 15:40:17

#統計このようにして、裾が太い分布による確率分布モデルで外れ値が出るケースをモデル化することの特別な場合として、中央値を見ることを理解できるわけです。

タグ：統計

posted at 15:42:13

#統計サンプル(母集団からの無作為抽出で得た有限の長さの数値列)について、平均(加法平均)や中央値を求めるときには、正規分布モデルもLaplace分布モデルも表に出て来ないので、確率分布モデルの存在が見えなくなってしまうのですが、やっていることはそういう特別なモデル依存の計算なわけです。

タグ：統計

posted at 15:47:17

#統計これは最小二乗法の場合も同じで、最小二乗法を使っている人が正規分布モデルを実質的に使っていることを認識できていなくても、最小二乗法が正規分布モデルという特殊なモデルを使った推定であるという事実から逃れることはできないわけです。

twitter.com/genkuroki/stat...

タグ：統計

posted at 15:53:15

RT 確率を議論するときに、頻度主義とか客観確率とかいう概念を作って難しく考える意味がわからない。

タグ：

posted at 16:05:31

昔２ちゃんねるかどこかで大きな議論になったことがあったわ。「トランプ１組５２枚から１枚取り出して別の場所に置いておく。残った５１枚から３枚取り出して見たら、すべてダイヤだった。最初のトランプがダイヤであった確率は？」っていうの。

タグ：

posted at 16:09:48

開いてないのが49枚で、そのうちダイヤは10枚だから、答えは10/49。でも「求める確率は最初に取り出したトランプに関することだから、後で見た3枚のダイヤは確率に影響しない、よって1/4」と譲らない人たちが大勢いたわ。

タグ：

posted at 16:13:36

#数楽以上は小学生でも分かるGauss-Bonnetの定理の解説スレッド pic.twitter.com/HX1YBF732w

タグ：数楽

posted at 16:14:40

そういう人って、事後確率とかベイズ主義とか、頻度主義とかいう概念を持ち出して、難しく難しく説明しようとするんだよね。でもそういう概念を使うことで何が嬉しいのか、ついぞわからなかった。

タグ：

posted at 16:17:08

おそらく「時系列で先に起こったか後に起こったか」を気にしてるんだろうけど、現実で起こることって、時系列順を気にしてたらものすごく大変になるだけだと思うんだけど。

タグ：

posted at 16:20:47

いちいち起こることを時系列順に並べて、順々に条件付き確率として求めていくの？簡単なものだったらいざ知らず、複雑な確率モデルだったら、そんなの計算してられないでしょ。

タグ：

posted at 16:23:10

#統計まさにそれ！

正しい確率は1/4だと言い張る人を連れて来て、仮に正しい確率が1/4なら公平になるルールで繰り返し俺と「勝負」してもらいたい(笑)。

なんぼでもカモれそうな感じ🤣

twitter.com/gcp_tama/statu...

タグ：統計

posted at 16:32:10

かめさん @cogitoergosumkm

たしかに確率論で間違ってるのに間違いを認めない人は簡単にカモれそうだなあとは思うよね twitter.com/genkuroki/stat...

タグ：

posted at 16:38:56

#統計私も同意見。

「頻度主義」「ベイズ主義」のような無用な考え方を学生に吹き込んではいけないと思うのですが、ベイズ統計が流行り始めたら、悲惨なことになってしまった。

ベイズ統計自体はこんなに楽しいのに！

社会的に責任を取るべき立場の人達が沢山いる。

twitter.com/gcp_tama/statu...

タグ：統計

posted at 16:46:31

#統計「どうして分散を求めるときに二乗を使うのですか？」はFAQ(よくある質問)なのですが、上の方に解説を読んだ人であれば二乗した場合の E[(X-μ)²] だけではなく、E[|X-a|] も役に立つことをすでに知っている。

E[(X-μ)²]を最小化するμがXの平均で、E[|X-a|] はaがXの中央値のとき最小になる。

タグ：統計

posted at 17:18:13

#統計学さすがに統計学入門で「中央値は重要ではない」とは言えるはずがないので、「二乗されていない単なる絶対値の場合の E[|X-a|] は重要でない」とも言えるはずがない。

この辺についても、多くの統計学入門の解説には不十分なところがあると思う。

タグ：統計学

posted at 17:21:40

「ミハジ」って、昔は邪道であると認識した上で後ろめたさを伴って学校外で教えられていましたよね。学校の先生があっけらかんと教えて、一部の学習塾が危機感を持って脱洗脳にまわる時代がくるとは、想像していませんでした。

タグ：

posted at 17:31:48

#統計平均値の代わりに中央値を見ることも立派な統計学なので、平均μと散らばり方の大きさの指標として分散 E[(X-μ)²] を使う代わりに、中央値 a と中央値からの距離の平均 E[|X-a|] を使うことも立派な統計学だと思います。

それらはそれぞれ、正規分布モデル、Laplace分布モデルの場合に対応。

タグ：統計

posted at 17:32:19

大石雅寿 @mo0210

女性自身も少しは学習したらいいのに。船瀬俊介の名前が出てきた時点でアレだということに。雑誌が売れればそれで良いのだろうなぁ。
headlines.yahoo.co.jp/article?a=2019...

タグ：

posted at 17:38:01

#統計平均μに対する E[|X-μ|] を持ち出して「使わない」とすることはちょっとミスリーディングだと思う。

「誤差」の指標が最小になるようにしたいのに、E[(X-μ)²] の対抗馬として、中央値ではなく平均値μに関する E[|X-μ|] を持ち出すのは奇妙な議論をしているように見えます。

タグ：統計

posted at 17:40:05

akmsk @a_akmsk

jupyter notebookなんて使わないと決めていたけど、使ってみたら使いやすかった。やらず嫌いはいかんな

タグ：

posted at 17:49:27

よこや @yaguramigigyoku

2023年からベクトル廃止して確率分布を必修にするの頭悪いやろ（）

タグ：

posted at 17:54:50

UFO教授 (藤木文彦 Fumihiko @UFOprofessor

#超算数これ、結構頭の痛い問題で、学生さんがバイトで「きはじ」「みはじ」「はじき」を

* よくできない子を助けるには効果的

のような理由で何の罪悪感も無しに教えているケースが少なくないものと思われます。

学生の段階で子供を傷付ける悪行を積んでしまっている。

twitter.com/kamo_hiroyasu/...

タグ：超算数

posted at 18:10:18

@kamo_hiroyasu @genkuroki 学習塾用教材の中にも、ミハジの図が書かれている物があり、学生バイトだけで無く、講師歴も長いはずの人がそれを使っているのを見るにつけ、こういうバカな教育法は、無くさないとならないと思います。（1人1人問題点を説明していても切りが無い。）

タグ：

posted at 18:11:03

CK @pantu_dorobow

朝日新聞(asahi shimbun） @asahi

小学校で〈みはじ〉を教えられたが、どうしてもその配置が覚えられなかった。
結局いつも「道のりは時間と速さの掛け算だから、"み"が上だな」とやってたけど、あれは人生で1番いらない時間だったのではなかろうか。 twitter.com/genkuroki/stat...

タグ：

posted at 18:29:14

囲碁名人戦、張栩名人が勝利　連覇に向けて好スタート t.asahi.com/wb3o

タグ：

posted at 18:50:03

@sekibunnteisuu 2013を203に書き落としちゃうのはまあ仕方ないですよ。それより参考文献表が黒崎東洋郎さんの名前を変な具合に間違っていました8254.teacup.com/kakezannojunjo...。

タグ：

posted at 19:02:33

ぎんなんまる @h84BxtzJwpCm1ru

朝日新聞名古屋編集局 @asahi_nagoya

殆どが東大志望の某私立進学校では、民間試験について、

『校長が証明書を書くから受けなくていいよー。みんなＡ２は満たしているから』と言われたそうです。既に高1までに民間試験を学校で受けてスコアは確認できてるし。

受験意識高い層が高みの見物的になるため、問題意識は今ひとつ広がらない。

タグ：

posted at 19:02:39

囲碁名人戦、張栩名人が勝利　連覇に向けて好スタート
www.asahi.com/articles/ASM8V...

タグ：

posted at 19:03:26

残り56件のツイートを見る

#超算数私、一般化話がとても苦手で、こんなことを書くときっと後で馬鹿を晒したことが発覚するのですが偉そうなことを言いたい衝動に負けて。この4人は #掛算についての態度においてあまり差がない。互いに或は派閥同士で批判していても、大正新教育の算数を継続しようとしている点で同じでないか。

タグ：掛算超算数

posted at 19:11:58

#超算数中島健三は意味説(meaning theory)が戦後算数教育に大きく影響したと言っていた。一方、遠山啓はピアジェの学説に多くを負うているようで、積分さん紹介の書籍は日本の算数を構成主義的と言っている。ただし、私の狭隘な料簡で見るところの意味説も構成主義も #掛算の順序を支持しはしない。

タグ：掛算超算数

posted at 19:18:23

#超算数だから、私は意味説も構成主義も、大正新教育の算数を、例えば学力低下論に抗して、貫徹するための旗印なのではないかと疑っています。戦前のその手の算数では例えば東京市や青木誠志郎の調査のように、掛順は減点対象でした。

タグ：超算数

posted at 19:22:21

朝日新聞文化部 @asahi_bunka

囲碁名人戦、張栩名人が勝利　連覇に向けて好スタート：朝日新聞デジタル www.asahi.com/articles/ASM8V...

タグ：

posted at 19:33:25

#統計あと、例えば「収入」などの統計では「中央値」に特別に興味がわくことが普通のことだと思うが、中央値(と中央値からの距離の平均)の推定がLaplace分布モデルによる推定であることを知った後だと、「え？Laplace分布に近い形の分布は珍しいよね！」と思わざるを得ません。続く

タグ：統計

posted at 19:47:34

クリスマスローズ　戦争反対 @educationmama3

#統計分布全体の形が大体わかっているなら、それなりにもっともらしい確率モデルをいくつか作ってフィッティングした結果を見た方がずっと色々なことが分かると思う。

現代ではコンピューター上で確率モデルを扱うことが相当に易しくなっていると思う。

タグ：統計

posted at 19:47:34

@h84BxtzJwpCm1ru それはありますよね・・・

だからこそ問題なのですが。

タグ：

posted at 19:47:38

#統計例えば、政府が政策的に、平均収入だけではなく、収入から得られる効用の平均にも気を使っているとき、その制限の下で「ランダム」に年収が決まるというモデルを考えると、一般にガンマ分布のような形の確率分布が出て来ることが分かります。収入Xの効用がlog Xに比例する場合が丁度ガンマ分布。

タグ：統計

posted at 19:57:05

#統計続き。1つ前のツイートの結果は統計力学でカノニカル分布が自然に出て来る仕組みの特殊化の一般化をKL情報量を使って扱えば出せます。(確率モデリングでもKL情報量の理解は重要)

効用函数をlog以外にすればガンマ分布以外に様々な分布が出て来る。

タグ：統計

posted at 19:57:05

ぎんなんまる @h84BxtzJwpCm1ru

上位の大学がＡ２を受験資格としたことが、そう意味では裏目に出たというか。
使わない選択をしてくれれば社会的にインパクトはあったのに。

実害を受ける層は、実はまだこの問題に気付いていない場合が多い。高3になってからが受験モードだから。その時点ではもう遅い、というのは制度が悪い。

タグ：

posted at 20:00:02

#統計現実の収入の分布のグラフを見ても、ガンマ分布っぽい形をしています。

より正確な言い方をすると、平均の上限と効用の平均の下限が与えられたとき、その制限の下で分布をランダムに決めるとガンマ分布っぽい分布が自然に出て来ることを数学的に示せます(KL情報量の1つの使い方)。

タグ：統計

posted at 20:00:47

@genkuroki #超算数　学生バイトどころか、陰山英男のような著名人までが、「はじき」を推奨している。何でこんな人が教育における権威と見做されてしまうんだろうか？

togetter.com/li/1310474

タグ：超算数

posted at 20:00:58

#統計効用の平均に下限を設ける政策は福祉政策の一種だとみなせるでしょう。

一方、平均だけに上限を設けた場合には、指数分布が自然に出て来ます(これはよく統計力学の教科書に載っています)。

で、収入ではなく、資産の分布を見ると、指数分布っぽい形をしていることが分かる。

タグ：統計

posted at 20:03:42

#統計資産分布が指数分布っぽい形をしているという事実は、「政府が資産から得られる効用の平均が下がりすぎないようにする(結果的に資産を何も持たない人が減る)」というような政策を一切行っていないことを示唆しています。

こういうことにもKL情報量は応用がある。

タグ：統計

posted at 20:06:30

#統計所得の分布がガンマ分布っぽい形をしていて、資産の分布が指数分布っぽい形をしていることについては、以下のリンク先の添付画像を参照。

twitter.com/genkuroki/stat...

タグ：統計

posted at 20:09:25

#統計平均に上限を設けるだけの制限で分布をランダムに決めると指数分布が出て来ることのコンピューターシミュレーション。

twitter.com/genkuroki/stat...

タグ：統計

posted at 20:12:32

#統計平均に上限を設けるだけではなく、効用に下限を設ける制限の下で分布をランダムに決めるとガンマ分布が出て来ることのコンピューターシミュレーション。ただし、効用函数としてlogを採用。(より一般には効用函数には上に凸な単調増加函数を取る。)

twitter.com/genkuroki/stat...

タグ：統計

posted at 20:15:35

#統計 KL情報量の話の分岐。カノニカル分布の話。以下、確率密度函数のことを確率分布や分布と呼んだります。

定義：事前分布がφ(w)のカノニカル分布とは

ψ(w) = Z(β)⁻¹ exp(-βH(w))φ(w)

のように書ける分布のことである。ここで

Z(β) = ∫ exp(-βH(w))φ(w) dw.

続く

twitter.com/genkuroki/stat...

タグ：統計

posted at 20:35:11

#統計逆温度β付きのベイズ統計では、サンプルX₁,…,X_nで決まる

H(w) = -Σ_{k=1}^n log p(X_k|w)= -(対数尤度函数)

を使います。このとき、カノニカル分布ψ(w)は

ψ(w) = Z(β)⁻¹ (p(X₁|w)…p(X_n|w))^β φ(w)

となり、ψ(w)は事後分布になります！

タグ：統計

posted at 20:41:16

#統計事前分布がφ(w)のカノニカル分布が統計力学的にもしくはKL情報量的に出て来る仕組みは以下の通りです。続く

タグ：統計

posted at 20:49:14

#統計

定理(ラフスケッチ)：事前分布φ(w)に従う長さnの乱数列W₁,…,W_nを条件

(1/n) Σ_{i=1}^n H(W_i) = c

で制限して得られる条件付き確率分布におけるW₁の分布は、n→∞で、カノニカル分布

ψ(w) = Z(β)⁻¹ exp(-βH(w))φ(w)

に近付く。逆温度βは ∫H(w)ψ(w)dw = c という条件から決まる。

タグ：統計

posted at 20:49:15

#統計統計力学の教科書では、物理的に等確率の原理を仮定しているので、事前分布が一様分布になって見えなくなっているのですが、教科書に書いてある内容の多くが自明に事前分布付きの場合に一般化されます。

タグ：統計

posted at 20:51:28

公式を暗記するか導出を暗記するかの二択という認知の歪みもあるのか。

タグ：

posted at 20:53:21

@kaitou_ryaku @physics303 #統計答えを書いておきました。

twitter.com/genkuroki/stat...

タグ：統計

posted at 20:53:31

梅崎直也 @unaoya

このツイートを参考にして、多面体のガウスボンネの定理についていくつかの計算例を紹介しました。 youtu.be/p6H3J2t4OVk via @YouTube twitter.com/genkuroki/stat...

タグ：

posted at 20:56:23

#統計自分でその自明な拡張(事前分布付きの場合へのカノニカル分布の拡張)をする手間を省きたければ、私による解説ノート

genkuroki.github.io/documents/2016...
Kullback-Leibler 情報量と Sanov の定理

の第2節や第7節を見てください。

タグ：統計

posted at 20:56:57

「導出を暗記」というのが意味わからん。どんな行為をそう呼ぶのだろう？

タグ：

posted at 20:57:29

#統計補足：第4節も。

タグ：統計

posted at 21:02:19

#統計分岐

twitter.com/genkuroki/stat...

タグ：統計

posted at 21:06:21

この種の、公式を丸暗記するか毎回導出するかの二択という認知の歪みは、よく見かけます。数学が分かっている人がやっていることはどちらでもないのに。 twitter.com/PTA58277795/st...

タグ：

posted at 21:12:57

導出を経験した結果なんとなく覚えたというのが、数学が分かっている人の普通です。

タグ：

posted at 21:12:58

「凡人は、公式を暗記する手段として導出を追いかけろ」がなぜ通じないか、理解できません。

タグ：

posted at 21:14:50

#統計 KL情報量の-1倍は、事前分布付きの場合の統計力学的な意味でのエントロピーそのものです。事前分布に対する相対的なエントロピーという意味で、相対エントロピーという言い方もあります。

KL(q|p) = -(事前分布pに対する分布qの相対エントロピー)

というような見方もできる。

タグ：統計

posted at 21:15:03

@genkuroki @physics303 ありがとうございます！

ベイズにおけるサンプルサイズは、統計力学の粒子数とは異なる概念という認識なのですが、黒木さんの意見をお聞かせ頂けるとありがたいです。
サンプルサイズは、ハミルトニアンに含まれるパラメタ(X1,...,Xn)の個数に対応し、物理の状態空間の次元は変えないという認識です

タグ：

posted at 21:15:07

「こんなに違う！　アジアの算数・数学教育」田中義隆　明石書店

気になる点は他にもあった。 pic.twitter.com/OaKnHbj7ms

タグ：

posted at 21:16:13

概数はトポロジーと関係してくるの？

素で分からない。もしかしたら私の認識不足で筆者が正しいのかもしれない。

誰か教えて欲しい。 pic.twitter.com/TCBq4FnXe3

タグ：

posted at 21:19:30

子どもを見くびりすぎなきがするけど・・・

　20人で山分けするのも21人で山分けするのもそんなには変わらない、ということを理解することは子どもには不可能なの？

　理解できない子もいるかもしれないが、理解できる子もいるんじゃないの？ pic.twitter.com/CYGXGB3bNz

タグ：

posted at 21:25:18

@paris74723668 だから数学の学習を放棄するというなら、まだわかるんですよ。わざわざ、凡人にはもっと辛くてつまらなくて時間がかかる丸暗記を選択するのが常人の理解を超えています。

タグ：

posted at 21:26:29

Re:RTs え！うっくん、あれを勝ったのか！勝負強過ぎ。

タグ：

posted at 21:28:40

@genkuroki @physics303 ベイズのサンプルサイズを増やすと、ハミルトニアンHの項の数が加算的に増えるので、統計力学の粒子数に対応しそうな気持ちになります

しかしこの対応は成り立たない気がしています。状態空間Wの次元が増えないからです。サンプルサイズの変化はHの値だけ変えて、Wは変化させない何かだと考えています

タグ：

posted at 21:30:54

非公開

タグ：

posted at xx:xx:xx

@genkuroki @physics303 あ、すいません、ツイートを読み返したら自己解決しました。 twitter.com/genkuroki/stat... この話が本質的ですね。私の気になっていたところです。ありがとうございました

タグ：

posted at 21:40:05

kifudepot.net/kifucontents.p...
第44期名人戦挑戦手合七番勝負第1局

❌棋聖戦→⭕️名人戦

タグ：

posted at 21:46:46

ベイズ統計と、物理の統計力学の関係で、この2年間しっくりこなかった部分が黒木さんのツイートを読んで解決しました。これは両者の関係を考える上で極めて本質的かつ重要かつ非自明な内容だと思うのですが、他所では見かけない気がする(僕は見たことない)。市場に流通する出版物には書いてなさそう twitter.com/genkuroki/stat...

タグ：

posted at 21:52:14

いや、しかしだ、黒木さんのツイートの内容を知らなければ、こういう考えに至るのもやむを得ない気がするぞ(自分の頭の悪さを棚に上げる)　twitter.com/kaitou_ryaku/s...

タグ：

posted at 21:54:55

闇のapj @apj

ごまふあざらし(GomahuAzaras @MathSorcerer

@Chief_Editor7 www.cml-office.org/wwatch/magne　の中程に、パイプテクターコーナーがあります。実験結果としては、横浜市水道局が試験的に導入し、設置数年後に検査したけど配管の錆は装置の上流と下流で差が無かったという結果が出ています。情報開示請求で試験結果全部もらって公開中です。

タグ：

posted at 22:30:31

チズチズ(Yuma Ochi) @chizu_potato

Gomahで変換したResNetさん元の実装のChainer並な速度でちゅらい。まだマシなのはcode warn で調べると赤文字真っ赤なので最適化の余地はあること

タグ：

posted at 22:44:57

OokuboTact　大久保中二病中年 @OokuboTact

学校の数学の授業で箱ひげ図やったんだけど、先生が何となくデータの特徴がわかりますとか言ってたんだけど分布の形が歪だった場合には対応できないしそこはヒストグラムを書いてやるべきだとも思った。
曖昧でも良いとか言われて？？？となっている
明日、また聞きに行くつもり

タグ：

posted at 23:03:05

ごまふあざらし(GomahuAzaras @MathSorcerer

@sekibunnteisuu 磯田氏の図は、わさっき氏のブログでも取り上げていますね、
わさっき氏は、「大谷泰照: 平成の廃仏毀釈日本語軽視の数学教育を憂う」というトンデモを紹介しています。
廃仏毀釈というおどろおどろしい題名ですが、
珍しい説ではなく、むしろ王道トンデモな説です

takehikom.hateblo.jp/entry/20140722...

タグ：

posted at 23:11:51

こんなのとか．FluxのなかでNNlib.jlのconvを呼び出すところで引っかかってそう．よく言えばFluxはまだ改善の余地がある． pic.twitter.com/YMYYf0KlJT

タグ：

posted at 23:16:49

高梨陣平 @jingbay

これ今頃、記事にしてきた割にGoogleの言い分だけを記事にしているのに泣けた。記事のタイトルで"?"を使うのを恥しいと考えて欲しい。その上でこの記者はWSJの次の記事を読んでGoogleの言ってる内容が正しいかどうか考えてまた記事を書き直して欲しい。www.wsj.com/articles/googl... twitter.com/madonomori/sta...

タグ：

posted at 23:18:57

Oguchi T／小口高 @ogugeo

海の波の撮影を得意とするオーストラリアの Chris Dixon 氏が自選した50枚の写真集。 bit.ly/2MKc5Kn シャッタースピードを非常に短く設定し、波が瞬間的に作る造形をとらえている。背後の空や日射の状況に応じて多様な色彩が生じている点も興味深い。読者の人気が高い写真ほど上位にある。 pic.twitter.com/SeTeQyMTlZ

タグ：

posted at 23:19:20

私による #Julia言語の典型的な使用パターン

(1) 単純な繰り返しで確認できそうな問題に出会う。
(2) 単純処理の10億回のループで十分そうか考える。
(3) 実際にJuliaでやってみる。

単純処理の10億回のループなら数秒で計算が終わる。

1ギガループ＝Juliaでの仕事の1単位

タグ： Julia言語

posted at 23:31:17